模型选择

1 偏差与方差

1.1 点估计

对参数$\theta$ 的一个预测，记为$\hat{\theta}$ ，假设$\left\{x_{1}, x_{2}, \cdots, x_{m}\right\}$ 是独立同分布的数s据点，该分布由参数$\theta$ 决定，则参数$\theta$ 的点估计为某个函数：

$$\hat{\theta}_{m}=g\left(x_{1}, x_{2}, \cdots, x_{m}\right)$$

频率学派：真实参数$\theta$ 是固定的，但是未知。$\hat{\theta_m}$ 是数据点的函数（可以用极大似然估计计算）。

1.2 偏差

偏差：学习算法的期望预测与真实结果的偏离程度，与真实世界的偏离。偏差衡量的是偏离真实值的误差的期望。

$$\operatorname{bias}\left(\hat{\theta}_{m}\right)=\mathbb{E}\left(\hat{\theta}_{m}\right)-\theta$$

高偏差 —— 欠拟合：模型有偏离。模型偏简单。

如果$\operatorname{bias}\left(\hat{\theta}_{m}\right)=0$ 则估计量$\hat{\theta_m}$是无偏的。如果$\lim _{m \rightarrow \infty} \operatorname{bias}\left(\hat{\theta}_{m}\right)=0$ 则估计量$\hat{\theta_m}$是渐进无偏的。

1.3 方差

方差：理解1，同样大小的训练集的变动所导致的学习性能的变化，接受不同数据后的模型输出的稳定程度。理解2，从潜在的数据分布中独立的获取样本集时，估计量的变化程度。理解3，方差衡量的是由于数据采样的随机性可能导致的估计值的波动。

$$\operatorname{Var}(\hat{\theta})$$

高方差 —— 过拟合：完全拟合训练数据。模型可能偏向复杂。

噪声表达了当前任务上任何学习算法所能达到的期望泛化误差的下界，也就是最小值。

eg：RF减少的是方差。Adaboost是减小偏差，尽量去拟合数据。

当交叉验证和测试集误差都很大的时候，怎么判断是bias problem还是variance problem呢？

bias problem：训练误差大，交叉验证误差大。

variance problem：则是训练误差小，交叉验证误差远远比训练误差大。

统计理论表明：如果训练集和测试集中的样本都是独立同分布产生的，则有 模型的训练误差的期望等于模型的测试误差的期望 。

机器学习的“没有免费的午餐定理”表明：在所有可能的数据生成分布上，没有一个机器学习算法总是比其他的要好。意思是特点任务的数据的分布往往满足某类假设，从而设计在这类分布上效果好的算法。

2 正则化

$$J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\frac{\lambda}{2 m} \sum_{j=1}^{m} \theta_{j}^{2}$$

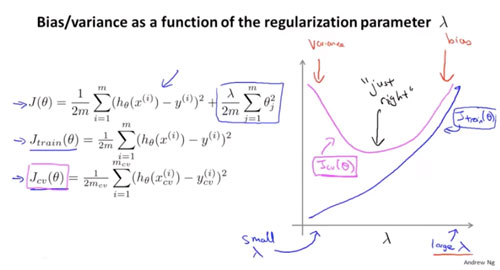
正则化中的$\lambda$和偏差，方差的关系。

训练误差：随着$\lambda$ 增大的时候，训练损失增大，$\lambda$ 太大的时候对参数惩罚过重，因此容易有高偏差问题。此时对训练集都无法很好拟合。当$\lambda$ 太小的时候，非常容易的去拟合训练集。

交叉验证集的误差：$\lambda$ 过大，欠拟合，高偏差时交叉验证的误差也很大。在最左边是高方差问题，$\lambda$ 小，对数据过拟合交叉验证的误差也很大。

3 学习曲线

3.1 曲线随样本量变化

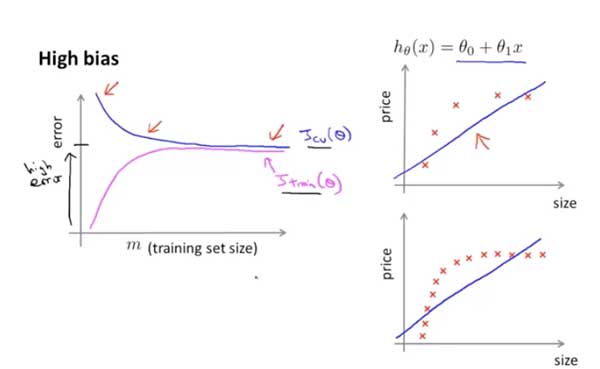
高偏差：训练误差随着样本数据逐渐增大。交叉验证误差随着样本数量减小（样本量越来越多无助于改善算法）。

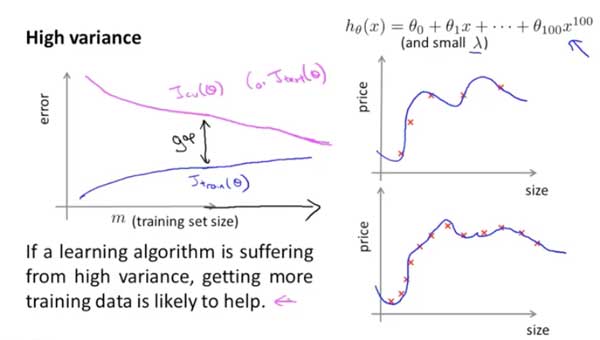
高方差：样本增大训练误差也增大，但相对而言误差小一点（因为一直在尽量拟合数据）。交叉验证的误差也慢慢下降，但总的来说样本越多训练得越好。

3.2 解决方法

高方差：缓解过拟合。

用更多数据训练（数据增强，更多训练数据），更少量的feature（做），增加正则项$\lambda$（贝叶斯估计中，正则化项对应于模型的先验概率$\log \frac{1}{g(\theta)}$），噪声注入（输入、输出、权重噪声等）、早停法。

高偏差：缓解欠拟合。

加更多的特征，减小正则项 $\lambda$ ，用更复杂的神经网络，对误分类的数据增加权重Adaboost。

3.3 误差分析

首先构建一个baseline，画出学习曲线，分析是否有高方差偏差的问题，关注那些被分错的数据（共同的特征和规律）。关注交叉验证的结果。

Reference

1， http://www.huaxiaozhuan.com/ 参考资料太棒了

2，吴恩达《机器学习》