SVM推导

1 简介

标签：二分类模型，特征空间上的间隔最大的线性分类器，核技巧（非线性问题），求解凸二次规划问题。

三类：线性可分支持向量机与硬间隔最大化，线性支持向量机与软间隔最大化，非线性支持向量机与核函数。

2 线性可分支持向量机

学习的目标是在特征空间中找出一个分离超平面，将实例分到不同的类。

$wx + b = 0$

$w$代表法向量，指向的一般是正类；$b$是截距。

利用误分类最小的策略求得分离超平面。利用间隔最大化求最优分离超平面。

在超平面确定的情况下，$|wx+b|$能够相对表示点$x$距离超平面的远近，$y (wx+b)$的符号是否一致表示分类是否正确。

2.1 函数间隔

1，函数间隔 $\hat{\gamma}_{i}=y_{i}\left(w \cdot x_{i}+b\right)$，超平面关于训练数据$T$ 的函数间隔 $\hat{\gamma}=\min _{i=1, \cdots, N} \hat{\gamma}_{i}$

函数间隔可以表示分类预测的正确性及确信度。

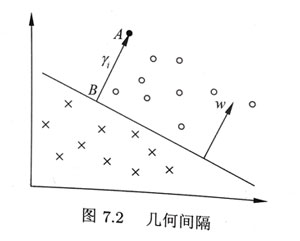
2，几何间隔：

对分离超平面的法向量 $w$加上某些约束，如规范化 $||w||=1$，使得间隔确定，这时函数间隔为几何间隔。

给定训练集$T$ 和超平面$(w,b)$，定义超平面关于样本点$(x_i,y_i)$的几何间隔是：

$\gamma_{i}=y_{i}\left(\frac{w}{\|w\|} \cdot x_{i}+\frac{b}{\|w\|}\right)$

2.2 间隔最大化

1，SVM基本思想

求解能够正确划分训练数据集并且几何间隔最大的分离超平面。

$\max _{w, b} \frac{\hat{\gamma}}{\|w\|}$ $\text { s.t. } \quad y_{i}\left(w \cdot x_{i}+b\right) \geqslant \hat{\gamma}, \quad i=1,2, \cdots, N$

函数间隔$\hat{\gamma}$ 不影响最优化问题的解，可以得到下面的线性可分支持向量机学习的最优化问题，凸二次规划问题，有最优解且唯一。（原始最优化问题）（备注，判断一个问题是否是凸问题，凸优化）

$\min _{w, b} \frac{1}{2}\|w\|^{2}$ $\text { s.t. } \quad y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N$

求解得到分离超平面：

$w^{*}·x+b^{*}=0$

分类决策函数是：

$f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right)$

2，支持向量

在线性可分情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量。支持向量是使约束$\text { s.t. } \quad y_{i}\left(w \cdot x_{i}+b\right)-1 = 0$ 成立。

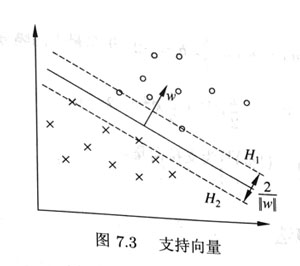
间隔等于$\frac{2}{||w||}$

2.3 对偶问题

通过求解对偶问题得到原始问题的最优解。

首先构建拉格朗日函数，不等式约束引入拉格朗日乘子 $\alpha_{i} \geqslant 0 , i=1,2, \cdots, N$

$L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{N} \alpha_{i} y_{i}\left(w \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i}$

其中 $\alpha=\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{N}\right)^{\mathrm{T}}$ 是拉格朗日乘子向量

需求$\max _{\alpha} \min _{w, b} L(w, b, \alpha)$

Step1，先求$\min _{w, b} L(w, b, \alpha)$

拉格朗日函数 $L(w, b, \alpha) $ 分别对$w,b$求偏导并令其等于0。

$\nabla_{w} L(w, b, \alpha)=w-\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i}=0$ $\nabla_{b} L(w, b, \alpha)=-\sum_{i=1}^{N} \alpha_{i} y_{i}=0$

代入回拉格朗日函数中 $L(w,b,\alpha)$ 并化简：

$L(w, b, \alpha)=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} y_{i}\left(\left(\sum_{j=1}^{N} \alpha_{j} y_{j} x_{j}\right) \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i}$

化简推导过程见[5]，也可以代入简单的例子去看，化简得到：

$\min _{w, b} L(w, b, \alpha)=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i}$

Step2，求$\min _{w, b} L(w, b, \alpha)$ 对$\alpha$的极大值，即是对偶问题：

$\max _{\alpha}-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i}$

转换为求极小

$\min _{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i}$ $\text { s.t. } \quad \sum_{i=1}^{N} \alpha_{i} y_{i}=0 , \alpha_i \geqslant 0$

注意：为什么线性规划中求解原始问题可以转为求解对偶问题，对偶问题有良好的性质。对偶问题的对偶是原问题，无论原始问题是否是凸对偶问题都是凸优化问题，对偶问题可以给出原始问题的一个下界，满足一定条件时原始问题的解与对偶问题的解是完全等价的（备注拉格朗日对偶问题）。

Step3，根据KKT条件求得 $w^{\star}$ 与 $b^{\star}$

过程如下，设 $\alpha^{\star}=\left(\alpha_{1}^{\star}, \alpha_{2}^{\star}, \cdots, \alpha_{N}^{\star}\right)^{\mathrm{T}}$ 是对偶最优化问题的解。根据原问题的不等式约束，KKT条件成立。

$\nabla_{w} L\left(w^{\star}, b^{\star}, \alpha^{\star}\right)=w^{\star}-\sum_{i=1}^{N} \alpha_{i}^{\star} y_{i} x_{i}=0$ $\nabla_{b} L\left(w^{\star}, b^{\star}, \alpha^{\star}\right)=-\sum_{i=1}^{N} \alpha_{i}^{\star} y_{i}=0$ $\alpha_{i}^{\star}\left(y_{i}\left(w^{\star} \cdot x_{i}+b^{\star}\right)-1\right)=0, \quad i=1,2, \cdots, N$ $y_{i}\left(w^{\star} \cdot x_{i}+b^{\star}\right)-1 \geqslant 0, \quad i=1,2, \cdots, N$ $\alpha_{i}^{\star} \geqslant 0, \quad i=1,2, \cdots, N$

由此可得:

$w^{*}=\sum_{i} \alpha_{i}^{\star} y_{i} x_{i}$

至少有一个$\alpha_i^{\star} > 0$，将$w^*$ 代入$y_{j}\left(w^{\star} \cdot x_{j}+b^{\star}\right)-1=0$ （注意 $y_j^2 = 1$）得:

$b^{\star}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{\star} y_{i}\left(x_{i} \cdot x_{j}\right)$

最终分类决策函数是：

$f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{\star} y_{i}\left(x \cdot x_{i}\right)+b^{\star}\right)$

《李航》书P125例子好

3 线性支持向量机与软间隔最大化

线性不可分问题（即某些样本点不满足函数间隔大于等于1的约束条件），用软间隔最大化（引入松弛变量）:

$y_i(w \cdot x_i + b) \geqslant 1 - \xi_i$

原始问题：

$\min _{w, b} \frac{1}{2}\|w\|^{2} + C \sum_{i=1}^N \xi_i$ $\text { s.t. } \quad y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1 - \xi_i, \quad i=1,2, \cdots, N$ $\xi_i \geqslant 0,i=1,2, \cdots, N$

对偶问题：

4 非线性支持向量机

核技巧。例子从椭圆变到线性可分，设原空间：$\mathcal{X} \subset \mathbf{R}^{2}, x=\left(x^{(1)}, x^{(2)}\right)^{\mathrm{T}} \in \mathcal{X}$，新空间 $\mathcal{Z} \subset \mathbf{R}^{2}, z=\left(z^{(1)}, z^{(2)}\right)^{\mathrm{T}} \in \mathcal{Z}$，从原空间到新空间的映射：$z=\phi(x)=\left(\left(x^{(1)}\right)^{2},\left(x^{(2)}\right)^{2}\right)^{\mathrm{T}}$