感知机 & KNN

1 感知机

1.1 简介

感知机是二分类线性分类模型，感知机对输入空间中将实例划分为正负两类的分离超平面，属于判别模型。使用基于误分类的损失函数，利用梯度下降法对损失函数进行最小化。

感知机：

$$f(x)=\operatorname{sign}(w \cdot x+b)$$ $$\operatorname{sign}(x)=\left\{\begin{array}{ll}{+1,} & {x \geqslant 0} \\ {-1,} & {x<0}\end{array}\right.$$

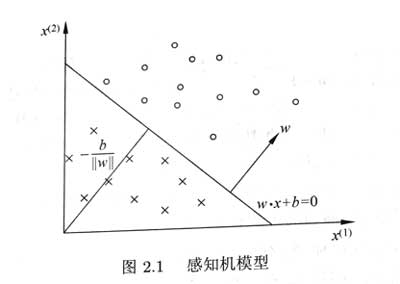
1.2 学习策略

损失函数的自然选择是误分类点的总数（但这样$w,b$不是连续可导函数，不易优化）

故采用误分类点到超平面$S$的总距离：

$$\frac{1}{\|w\|}\left|w \cdot x_{0}+b\right|$$

由于对于一个误分类的数据$(x_i,y_i)$来说：

$$-y_i(w \cdot x_i + b) > 0$$

因此感知机的损失函数是（忽略常数）：

$$L(w, b)=-\sum_{x_{i} \in M} y_{i}\left(w \cdot x_{i}+b\right)$$

1.3 随机梯度下降

一次随机选取一个误分类点使其梯度下降。

损失函数的梯度：

$$\nabla_{w} L(w, b)=-\sum_{x_{i} \in M} y_{i} x_{i}$$ $$\nabla_{b} L(w, b)=-\sum_{x_{i} \in M} y_{i}$$

选取一个误分类点$(x_i,y_i)$进行更新w，b。

$$w = w + \alpha y_i x_i , b = b + \alpha y_i$$

1.4 感知机算法过程

输入：训练数据集$T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}$，其中$x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_i \in y=\{-1,+1\}, i=1,2, \cdots, N$ 。学习率 $\alpha$，

输出： 求解感知机模型 $f(x) = sign(w \cdot x + b)$

(1) 选取初值$w_0,b_0$

(2) 在训练数据中选取数据 $(x_i,y_i)$

(3) 如果$y_{i}\left(w \cdot x_{i}+b\right) \leqslant 0$ ，则 $w = w + \alpha y_i x_i, b = b + \alpha y_i$

2 K近邻KNN

2.1 简介

KNN是一种基本的分类与回归方法。KNN法假设给定一个训练数据集，其中实例类别已定。分类时，对新的实例根据其K个最近邻的训练实例的类别，通过多数表决来预测。

基本要素：K值的选择，距离度量，分类决策规则

2.2 K近邻法算法

输入：训练数据集$T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}$，其中 $x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_i \in y=\{c_1,c_2,\cdot \cdot, c_k\}, i=1,2, \cdots, N$

输出：新实例 $x$ 所属的类别 $y$

(1) 根据给定的距离度量，在训练集中找出与x最临近的k个点，涵盖这k个点的x的邻域记作$N_k(x)$

(2) 在$N_k(x)$中根据分类决策规则（如多数表决）来判定x的类别y

$$y=\arg \max _{c_{j}} \sum_{x_{i} \in N_{k}(x)} I\left(y_{i}=c_{j}\right), \quad i=1,2, \cdots, N ; j=1,2, \cdots, K$$

$I$是指示函数，当$y_i = c_j$ 时为1。

2.3 距离度量

距离是两个点相似度的反映。设特征空间$\mathcal{X}$是n维实数向量空间$\mathbf{R}^{n}$,

$$x_{i}, x_{j} \in \mathcal{X}, x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \cdots, x_{i}^{(n)}\right)^{\mathrm{T}}$$ $$x_{j}=\left(x_{j}^{(1)}, x_{j}^{(2)}, \cdots, x_{j}^{(n)}\right)^{\mathrm{T}}$$

则P范数距离是：

$$L_p(x_i,x_j) = ( \sum_{l=1}^n |x_i^{(l)} - x_j^{(l)}|^p)^{\frac{1}{p}}$$

p=1 曼哈顿距离，p=2 欧氏距离，p=$\infty$，是切比雪夫距离，各个坐标距离的最大值。

$$L_{\infty}\left(x_{i}, x_{j}\right)=\max _{l}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|$$

2.4 K值的影响

1，k较小时，使用较小的邻域中的训练实例进行预测，“学习”的近似误差减小，但是估计误差增大。即预测结果对邻近点非常敏感，如果邻近的点是噪声则会预测出错（容易过拟合）。

2.5 分类决策规则

一般多数表决。误分类的概率是：

$$P(Y \neq f(X))=1-P(Y=f(X))$$

则误分类率是：

$$\frac{1}{k} \sum_{x_{i} \in N_{k}(x)} I\left(y_{i} \neq c_{j}\right)=1-\frac{1}{k} \sum_{x_{i} \in N_{k}(x)} I\left(y_{i}=c_{j}\right)$$

2.6 k-d tree

为了提高k近邻的搜索效率。用特殊的结构存储训练数据，减少计算距离的次数。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分（递归），构成一系列的k维超矩形矩阵区域。（李航书P53）

搜索：首先找到包含目标点的叶节点，然后从该叶节点出发依次回退到父节点，不断查找与目标点最邻近的节点。当确定不存在更近的结点时终止。

Reference

1，《统计学习方法》李航