1 简介
集成学习(Ensemble learning)通过组合几种模型来提高机器学习的效果。构建并结合多个学习器,个体学习器要“好而不同”,一定的准确性/多样性。
2 提升方法
2.1 提升方法之Adaboost
一般过程:训练—基学习器—调整训练样本分布—重复得到更多基学习器 T个—将这T个基学习器加权结合。代表是Adaboost:提高那些被前一轮弱分类器分错的样本的权值。最后加权多数表决方法、加大分类误差率小的弱分类器的权值。属于序列集成。
算法(书P156):
输入训练集$T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}$,其中实例$x_{i} \in \mathcal{X}=\mathbf{R}^{n}$,$y_i \in \mathcal{Y} = \left\{ -1,+1 \right\}$
1,初始化训练数据的权值分布为均匀分布 。$w_{1i} = \frac{1}{N}$。
2,使用具有权值分布的$D_m$的训练数据集学习得到基分类器$G_{m}(x): \mathcal{X} \rightarrow\{-1,+1\}$。
3,计算$G_m(x)$在训练数据集上的分类误差率:
计算得到$G_m(x)$的系数,它表示了$G_m(x)$在最终分类器中的重要性。他随$e_m$的减小而增大。
在更新训练数据集的权值分布
其中$Z_m$是规范化因子:
4,构建基分类器的线性组合 $f(x) = \sum_{m=1}^M \alpha_m G_m(x)$
得到最终分类器:
2.2 提升方法之提升树 Boosting
采用加法模型(基函数的线性组合,基函数为树的时候叫Boosting tree),前向分步算法。减小偏差。
2.2.1 前向分步算法:
1,确定初始提升树$f_0(x) = 0$
2,第m步的模型是$f_m(x) = f_{m-1}(x) + T(x: \theta_m)$
这里需要通过经验风险极小化来确定下一棵决策树参数参数:
不同问题的提升树学习算法区别在于使用的损失函数不同。
| 问题 | 学习算法 |
|---|---|
| 回归树 | 平方误差(拟合残差) |
| 分类问题 | 指数损失函数 |
| 一般决策问题 | 一般损失函数 |
对于二分类问题,提升树算法只需将Adaboost算法中基本分类器限制为二分类树即可。
2.2.2 回归问题的提升树,拟合残差
1,初始化$f0(x)=0$
2,对m=1,2..M计算残差,N是样本数。当前模型拟合数据的残差。
拟合残差$r_{mi}$学习一个回归树$T(x: \theta_m)$。更新:
3,得到回归问题提升树
2.2.3 一般决策问题GBDT
一般损失函数:
梯度提升gradientBoosting (GBDT):利用最速下降法的近似方法,关键是利用损失函数的负梯度在当前模型的值
作为回归问题提升树算法中的残差的近似值,拟合一个回归树。
过程:
输入训练集$T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}$,其中实例$x_{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}, y_{i} \in \mathcal{Y} \subseteq \mathbf{R}$
输出回归树: $\hat{f(x)}$
(1) 初始化
(2) 对m = 1,2…M
对 i = 1,2,…N 计算:
对$r_{mi}$ 拟合一个回归树。得到第m棵树的叶节点区域$R_{m j}, j=1,2, \cdots, J$
对 j = 1,2 …J 计算:
更新
(3) 得到回归树
2.3 其他
XGBoost:
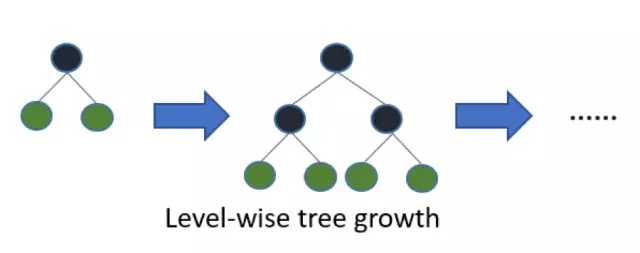
经过优化的分布式梯度提升(Gradient Boosting)库,实现了并行方式的决策树提升(Tree Boosting)。XGBoost采用的是level(depth)-wise生长策略,如下所示,能够同时分裂同一层的叶子,从而进行多线程优化,不容易过拟合;但不加区分的对待同一层的叶子,带来了很多没必要的开销。
XGBoost使用的是pre-sorted算法,能够更精确的找到数据分隔点;XGBoost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
XGBoost在代价函数里加入了正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。
LightGBM:
LightGBM的设计思路主要是两点:1. 减小数据对内存的使用,保证单个机器在不牺牲速度的情况下,尽可能地用上更多的数据;2. 减小通信的代价,提升多机并行时的效率,实现在计算上的线性加速。
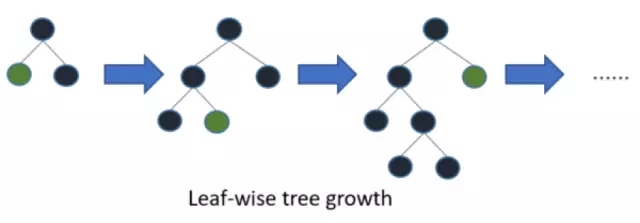
LightGBM采用leaf-wise生长策略,如Figure 2所示,每次从当前所有叶子中找到分裂增益最大(一般也是数据量最大)的一个叶子,然后分裂,如此循环;但会生长出比较深的决策树,产生过拟合。
LightGBM使用的是histogram算法,占用的内存更低,数据分隔的复杂度更低。
3 Bagging
3.1 Bagging
Bagging是有放回样本采样boostrap——产生互相有交叠的采样子集63.2% 。一般对分类任务使用简单投票法。剩下36.8%的数据可以用作验证集对泛化性能进行包外估计out-of-bag-estimate。
在不同样本集上训练不同的树,通常分类任务使用投票的方式集成,而回归任务通过平均的方式集成。减小方差。
3.2 随机森林
随机森林:样本采样+属性采样构建多棵决策树,最终决定结果。方差小,偏差也小。
4 Stacking方法
Stacking是通过一个元分类器或者元回归器来整合多个分类模型或回归模型的集成学习技术。基础模型利用整个训练集做训练,元模型将基础模型的特征作为特征进行训练。
其实就是先训练多个初级分类器,然后基于初级分类器对样本预测,将预测值作为新的训练集训练次级学习器。

Reference
1,李航《统计学习方法》

