1 笨笨的孩子慢慢学stay hungry stay foolish 2 学习，思考，实践，改变

0%

20191216面试1&图论问题回顾

发表于 更新于 分类于 Valine：

1，一面

第一次面试，居然去面了目前北京最火的一家公司，虽然不是我想去的算法岗。emmm，真的是胆大。不过一面的面试官超级可爱，很温和，我也太幸运了吧。先让自我介绍，然后问项目，然后出了一个很简单的算法题。

1.1 图论问题

项目是我大三做的一个图论赛题，回顾总结一下。

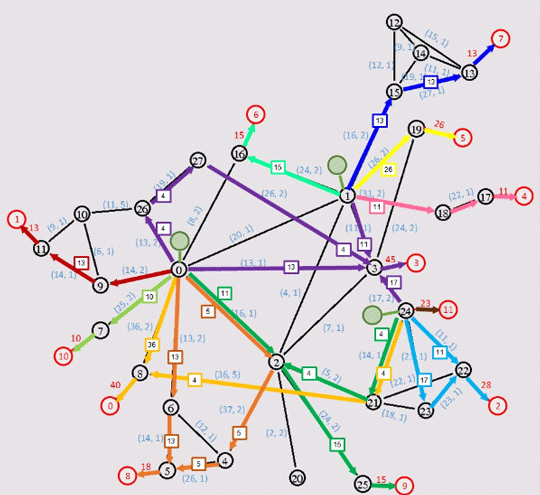
问题：“服务器选址问题”，从图中选出一些节点安放服务器（图中绿色节点 表示为$S_i$），服务器输出流量供给消费节点（图中红色节点，表示为$C_i$）

目标：第一要满足每个消费节点的流量需求，第二费用最小。

约束：每个路径有流量限制$flow_{constrain}$，但上下行都可以。也有流量单位费用$UnitCost$。举例子比如图右上角从1到15节点，留出流量13，则费用是13 * 2 = 26，此条路后面只能再流过16 - 13 = 3的流量了。另外其他限制是90秒内必须输出结果，否则没有成绩，使用内存不超过2GB。

输出：每条路径，及流过的流量。

20170305HuaWeiFlow

1.2 我的算法

策略1：选择前n个可以流出带宽最大的节点

1，选择n个可以流出带宽最大的节点

step1 计算每个结点可以输出的带宽之和

step2 排序

step3 选择前n个，放置服务器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int getServerlocation(Graph& g,int* server)//bigest bandwith Id
{
    int location=0,i,bandwidth=0,SecondBandWidth=0;
    for(i=0;i<g.numV();i++){
        if(g.Bandwidth[i] > bandwidth){
            SecondBandWidth = bandwidth;
            location = i;
            bandwidth = g.Bandwidth[i];
        }
    }
    for(i=0;i<g.numC();i++)
    {
        if(location == server[i]){
            for(i=0;i<g.numV();i++){
                if(g.Bandwidth[i] == SecondBandWidth)
                    location = i;
            }
        }
    }
    return location;
}

step4 用Dijkstra计算服务器到消费节点的最短路径（只根据$flow_{constrain}$来计算），计算这条路径的可以流过的最大流量，分配流量，计算费用。

Dijkstra算法：

1
2
3
for(w=0;w<g.CountsOfConnectNode[v];w++){
	if (D[w] > D[v] + g.getUnitConsumeCost(v, w))  计算server到各个点的距离，判断并更新
		D[w] = D[v] + g.getUnitConsumeCost(v, w);

获取本条路径可以流过的最大流量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int getflow(Graph* G,int path[maxN][maxN],int cn)//get cn-consumenode minflow
{
    int flow = 0;
    int Cnode  = G->Con_Nodes[cn];
    int minflow = INFINITY,i;
    for(i=0;i<maxN;i++){
        if(minflow > G->getWeight(path[Cnode][i], path[Cnode][i+1])){
            minflow = G->getWeight(path[Cnode][i], path[Cnode][i+1]);
        }
        if(path[Cnode][i+2] == -1){
            flow = minflow;
            break;
        }
    }
    if(flow > G->Demand[cn])
        flow = G->Demand[cn];
    return flow;
}

更新图和消费节点的流量需求。

反过来消费点去找离他最近的服务器节点，分配流量。

策略2：实在不行选择与消费点的直连点放服务器。
1
2
3
4
5
6
7
8
9
10
/* server is in the consumenode */
   for(i=0;i<graph.numC();i++){
       if(server[ser-1] == graph.Con_Nodes[i]){
           pathpath[pathi][0] = server[ser-1];  //add to the answer
           pathpath[pathi][1] = i;
           pathpath[pathi][2] = graph.Demand[i];
           pathi++;
           graph.Demand[i] = 0;
       }
   }

1.3 其他方法

整数规划模型

启发式算法（模拟退火，遗传算法，去网上找了资料学了点基础）

当年的反思

20191218HuaWeiRes

1、一个类里面空间是有限的，如果开了几个1000*1000的二维数组是不行的，要么static，要么设置全局。

2、在Dijkstra 里CountsOfConnectNode不能因为单边减少而减一，因为单边减少就减一的话会造成无法访问一些边，因为我是先遍历的在判断的周边路径是否存在，即weight > 0。

3、一些存DotId的数组我初始化为了-1，其实-1是很容易造成下标越界的，但本来dot的范围是0~maxN，所以造成后面很多的判断 ！= -1 ，希望大家引以为戒。（因为-1 ，我的graph里的成员变量servercost竟然从100变成了-1，就是因为-1下标的范围导致内存访问异常，数据被修改，当时真是急哭我了）

4、记住所有变量定义的时候一定初始化，否则为任意值的话会造成不可知的错误，只能一直debug一步步找变量的变化，真是心累。

5、如果你的数据很多，请注释每个的含义，包括下标，否则你的队友会看不懂你的代码，自己写一写的就会弄混。

6、算法上的缺陷

没有反馈：一直计算的出来的结果，没有经过比较选择这是缺乏了优化的过程的。应该要一直迭代，随机取、放一些服务器后就算一遍最短路径和成本进行比较取优。其实我的代码跑完整个用的时间是ms级的，那么其实还要很多时间可以进行计算。因为最后来不及了也就没有做，自然成本高。

7、团队分工：队友要充分合作（一个人再强大真的比不上三个臭皮匠）、分工写任务，一定要充分相信对方。队长要想好整体，再把模块分开写，把需求明确，免得最后代码合并要哭。

8、编程基本功：编程基本功要多写多练才扎实，不然写这样的复杂稍大的程序就很容易出现一些低级错误

9、多去学习大佬怎么做的，站在前人大佬的基础上才不会自己太犯傻，至少基本的方向不会错！

2，算法题

1，写出二叉树的最短路径长度。长度 = 路径上节点的值的和。

1
2
3
4
int MaxPath(TreeNode* root){
	if (root -> NULL) return 0;
	else return root->val + max(MaxPath(root->left),MaxPath(root->right));
}

2，给出一个数组[1 3 2 6 5 7 10]，找出后面的比他大的第一个值，返回下标，答案 [1 3 3 5 5 6 -1]。

思路：倒过来遍历，取一个最小的stack

倒着遍历，维护一个递减的stack(top保持最小）。先10和其index绑定入stack，然后轮到7，判断stack top，若大于7就把stack top的数的index返回，否则弹出stack top，直到找到大于7或者stack弹空，若弹空则返回-1.然后把7绑定index压到stack里。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <stdio.h>
#include <iostream>
#include <stack>
using namespace std;

struct ListNode{
    int value;
    int index;
    ListNode(int a,int b)
    {
        this->value=a;
        this->index=b;
    };
};

int main(){
    stack<ListNode> stk;
    stack<int> res;
    int N; //N > 0
    cin>>N;
    int arr[N];
    for (int i=0; i<N; i++) {
        cin>>arr[i];
    }
    
    //algotithm
    res.push(-1);
    ListNode temp(arr[N-1],N-1);
    stk.push(temp);//put last value,arr[N-1]
    
    for (int i=N-1; i>=0; i--) {
        while ( !stk.empty()) {
            if (arr[i] < stk.top().value) {//compare with stack top value
                res.push(stk.top().index);//remember the result
                ListNode temp(arr[i],i);
                stk.push(temp);//put current arr[i]
                break;
            }
            else{
                stk.pop();
                if (stk.empty()) {
                    res.push(-1); //no bigger data, so res is -1
                    ListNode temp(arr[i],i); //put this value in it
                    stk.push(temp);
                    break;
                }
            }
        }
    }
    
    for (int i=0; i<N; i++) {//print the result
        cout<<res.top()<<endl;
        res.pop();
    }
  	return 0;
}

3 第二次zj开发岗

其实实习面试都是很基础的，本科学过的东西。问的主要是关于计算机网络，操作系统和数据库的。

操作系统。虽然目前开发岗

操作系统

1，线程和进程的区别：进程是运行中的程序，允许将多个程序调入内存并发执行，包含文本段、程序计数器、寄存器等。进程是CPU使用的基本单位，由线程ID、程序计数器、寄存器、栈等组合，与属于同一进程的其他线程共享代码段。

2，进程调度算法：先来先服务算法。短进程优先调度算法，优先权算法（非抢占、抢占式），高响应比优先调度算法。基于时间片的轮转法。多级反馈队列调度算法。

计算机网络

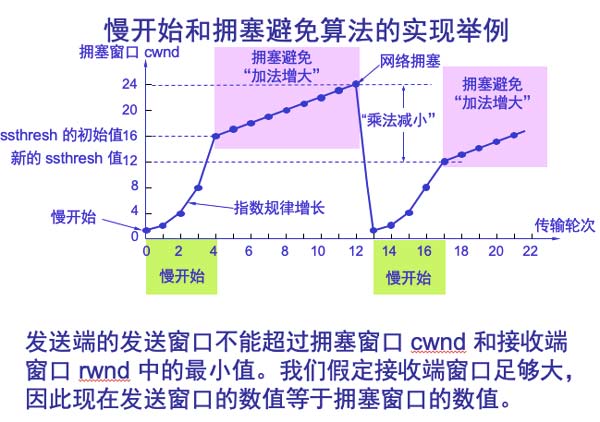
1，拥塞控制：发送方维护一个拥塞窗口，网络没有出现拥塞则拥塞窗口增大些，以便将更多的分组发送出去。但只要网络出现拥塞，就减小点。最开始cwnd窗口大小加倍，每收到一个对新的报文段确认后，将拥塞窗口加1。当cwnd < ssthresh 时，使用慢开始算法。> 则改用拥塞避免方法。当发送方判断网络出现拥塞，就把慢开始门限ssthresh设置为出现拥塞时的发送方窗口值的一半，然后cwnd重新设置为1，执行慢开始。

20170305HuaWeiFlow

数据库

1，数据库的三范式：1NF是不可分的基本数据项（即列不能够再分成其他几列，每列保持原子性） 。2NF不存在非主属性部分依赖于码。非主键列必须直接依赖于主键，不能存在传递依赖。每列都和主键相关。3NF非主键列是直接依赖于主键。

2，创建表：表名，字段名，类型，大小，完整性约束（主键 not null）

算法设计

给一批int数，要求实现一个数据结构，使得以下操作平均时间复杂度都为O(1)，增加、删除指定的数、随机获取一个数。（想了想其实数组的增加，查找是直接根据下标的很快。加上hash的删除指定数就可以了）