Stochastic Gradient Descent

1 概述

1.1 梯度下降

梯度下降是经典的局部优化算法。在2000年L Bottou使得随机梯度下降再次被提出。

对于数据$\left\{\left(X_{j}, Y_{j}\right)\right\}_{j=1}^{M}$ 需要求解：

$\min _{\theta \in \mathbb{R}^{n}} J(\theta), \quad J(\theta)=\frac{1}{M} \sum_{j=1}^{M} L\left(\theta ; X_{j}, Y_{j}\right)$

梯度下降迭代格式：

$\theta_{i+1}=\theta_{i}-\alpha_{i} \nabla J\left(\theta_{i}\right), \quad \alpha_{i} \in \mathbb{R}^{+}$

直接针对损失函数的梯度下降存在的问题是容易陷入局部极小，计算量大（每一次都要计算$\nabla_{\theta} L\left(\theta_{i} ; X_{j}, Y_{j}\right)$）, 鞍点终止问题（鞍点梯度为0）。

1.2 随机梯度下降

因此提出随机梯度下降。每次仅仅随机取一个数据$\left(X_{R_{i}}, Y_{R_{i}}\right)$来近似均值的损失$\frac{1}{M} \sum_{j=1}^{M} \nabla_{\theta} L\left(\theta_{i} ; X_{j}, Y_{j}\right)$。

$\theta_{i+1}=\theta_{i}-\alpha_{i} \nabla_{\theta} L\left(\theta_{i} ; X_{R_{i}}, Y_{R_{i}}\right)$

1.3 三种梯度下降

梯度下降：全部数据迭代计算梯度。

$\theta_{i+1}=\theta_{i}-\alpha_{i} \frac{1}{M} \sum_{j=1}^{M} \nabla_{\theta} L\left(\theta_{i} ; X_{j}, Y_{j}\right)$

随机梯度：随机取一个数据来更新梯度。

$\theta_{i+1}=\theta_{i}-\alpha_{i} \nabla_{\theta} L\left(\theta_{i} ; X_{R_{i}}, Y_{R_{i}}\right)$

小批量梯度：随机取$m(\in[50,300])$ 个数据来计算梯度。

$\theta_{i+1}=\theta_{i}-\alpha_{i} \frac{1}{m} \sum_{j=1}^{m} \nabla_{\theta} L\left(\theta_{i} ; X_{R_{i, j}}, Y_{R_{i, j}}\right)$

下批量梯度下降的好处。加噪，避免梯度法终止于鞍点，存在一定概率跳出局部极小，小批量计算量可接受。

如果$J_M(\theta)$满足强凸条件，对于批量梯度法，线性收敛。对于随机梯度下降法，次线性收敛。

1.4 Github代码

https://github.com/saruagithub/AIcourse_gradientDescent

2 SGD技巧

1，SGD缺点：梯度方向不一定好，固定的学习率太小收敛慢太大则阻碍收敛，如何快速穿过山谷（狭窄山谷的震荡）平原呢。

$v_i = \alpha \nabla_{\theta} J\left(\theta_{i}\right)$ $\theta_{i+1}=\theta_{i}-v_{i}$

2，动量法：梯度的加权平均，递归的添加方向的历史信息（即$v_{i-1}$）。但转弯会慢。

$v_{i}=\gamma v_{i-1}+\alpha \nabla_{\theta} J\left(\theta_{i}\right)$

其中$\gamma$ 是阻力因子。

$\theta_{i+1}=\theta_{i}-v_{i}$

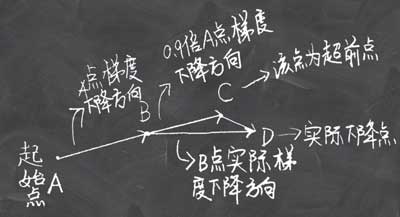
3，Nesterov：加速梯度法，更早的注意到梯度的变化。在动量法梯度更新前减去动量项。

$v_{i}=\gamma v_{i-1}+\alpha \nabla_{\theta} J\left(\theta_{i}-\gamma v_{i-1}\right)$ $\theta_{i+1}=\theta_{i}-v_{i}$

就是使用上一步的$v_{i-1}$先走一步再计算合并梯度。这里的$- \gamma v_{i-1}$就是下图B-C这段。

优点：前瞻性，在原方向虚拟走了一步后的梯度。收敛速度明显加快。波动也小了很多。

4，Adagrad：自适应梯度，弱化频繁变化的参数。$G_i$指的是历史与当前梯度的平方的累加。

$\theta_{i+1}=\theta_{i}-\frac{\alpha}{\sqrt{G_{i}+\epsilon}} \nabla_{\theta} J\left(\theta_{i}\right)$ $G_{i}=G_{i-1} + (\nabla_{\theta} J\left(\theta_{i}\right))^{2}$

$\epsilon$ 平滑项，避免除数为0。

5，RMSProp，对AdaGrad的一种改进，使用加权平均于梯度平方项。当前梯度平方项加上上一时刻的平均值。

$G_{i}=\gamma G_{i-1}+(1-\gamma)(\nabla_{\theta} J\left(\theta_{i}\right))^{2}$ $\theta_{i+1}=\theta_{i}-\frac{\alpha}{\sqrt{G_{i}+\epsilon}} \nabla_{\theta} J\left(\theta_{i}\right)$

另一个改进是定义指数衰减均值，AdaDelta2使用Delta平方的exponential moving average替代learning rate。

$\theta_{i+1} = \theta_i -\frac{\sqrt{D_{i-1}+\epsilon}}{\sqrt{G_{i}+\epsilon}} \nabla_{\theta} J(\theta_{i})$ $D_{i}=\gamma D_{i-1}+(1-\gamma)\left[\Delta \theta_{t}\right]^{2}$ $G_{i}=\gamma G_{i-1}+(1-\gamma)(\nabla_{\theta} J\left(\theta_{i}\right))^{2}$ $\Delta \theta_{t}=\theta_{t}-\theta_{t-1}$

6，Adam:Adam是对Momentum和RMPprop的一个结合。像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 vt 的指数衰减平均值，也像 momentum 一样保持了过去梯度 mt 的指数衰减平均值。

首先令：

$v_{i}=\gamma_{1} v_{i-1}+\left(1-\gamma_{1}\right) \nabla_{\theta} J\left(\theta_{i}\right)$ $u_{i}=\gamma_{2} u_{i-1}+\left(1-\gamma_{2}\right) (\nabla_{\theta} J\left(\theta_{i}\right))^{2}$

则：

$\hat{v}_{i}=\frac{v_{i}}{1-\gamma_{1}^{i}}, \quad \hat{u}_{i}=\frac{u_{i}}{1-\gamma_{2}^{i}}$

最终得：

$\theta_{i+1} = \theta_i - \frac{\alpha}{\sqrt{\hat{u}_{i}+\epsilon}} \hat{v}_{i}$

梯度部分像Momentum里一样使用V即梯度的exponential moving average来替代当前梯度来更新权重。学习率部分像RMSprop里一样用学习率除以S(即梯度的exponential moving average)来进行学习。V和S都初始化为0。一般$\alpha=0.001, \quad \gamma_{1}=0.9, \quad \gamma_{2}=0.999, \quad \epsilon=10^{-8}$

7, 推荐技巧：

$v_{i}=\gamma v_{i-1}+(1-\gamma) \nabla_{\theta} J\left(\theta_{i}-\gamma v_{i-1}\right)$ $u_{i}=\gamma u_{i-1}+(1-\gamma)\left(\nabla_{\theta} J\left(\theta_{i}-\gamma v_{i-1}\right)\right)^{2}$ $w_{i}=\gamma w_{i-1}+(1-\gamma) \Delta \theta_{i}^{2}$

可得：

$\theta_{i+1}=\theta_{i} -\frac{\sqrt{w_{i-1}+\epsilon}}{\sqrt{u_{i}+\epsilon}} v_{i}$

所有技巧的目的都是为了根据历史梯度和当前梯度来更新梯度。学习率迭代则是为了能适应梯度，梯度太大则更新小，将学习率learning rate除以当前的梯度，就能得到一个“适应”好的学习率的值。

数学回顾：一元函数的导数与泰勒级数

函数f(x)在x0上的导数定义为：

$f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}$

f(x)在x0附近的Taylor级数是：

$f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2}\left(x-x_{0}\right)^{2}+O\left(\left|x-x_{0}\right|^{3}\right)$