卷积神经网络CNN

1 图像基础

1.1 位图与矢量图

位图称为点阵图像、像素图或栅格图像，是由称作像素（图片元素）的单个点组成。他的单位是像素。位图有个缺点是放大后看到边缘是有些模糊的，这就是因为像素点组成的缘故。

位图的参数有：

像素：像素大小决定图像大小。

深度：色彩位数，每个像素使用的信息位数越多，可用的颜色就越多

通道：通常把RGB三种颜色信息称为红通道、绿通道和蓝通道，相应的把透明度称为Alpha通道，alpha通道存储图片的明暗信息等

矢量图的图形元素（点和线段）称为对象，每个对象都是一个单独的个体，它具有大小、方向、轮廓、颜色和屏幕位置等属性。矢量图形软件就是用数学的方法来绘制矩形等基本形状，因此它放大后不会模糊。

1.2 图像特征

图像具有视觉特征，即颜色、纹理、形状等。还具有空间关系特征，即物体与物体之间的空间关系等等（目前的研究热点 目标检测 yolo网络等）。

目前的卷积网络就是基于位图的，基于像素值、深度、通道等数值进行的计算。

2 卷积核

2.1 卷积介绍

卷积核其实是一个小的方阵。训练过程中的参数。

$$\left(\begin{array}{ccc}{1} & {0} & {1} \\ {0} & {1} & {0} \\ {1} & {0} & {1}\end{array}\right)$$

卷积的意义？

卷积运算就是在数据矩阵上做滑动的内积（向量内积是向量模长×cos夹角）。他的直观意义就是卷积核和图像的相似程度（余弦距离），可以发现局部的特征在什么位置明显，输出的feature map则提现了图片局部与卷积核的相似程度。

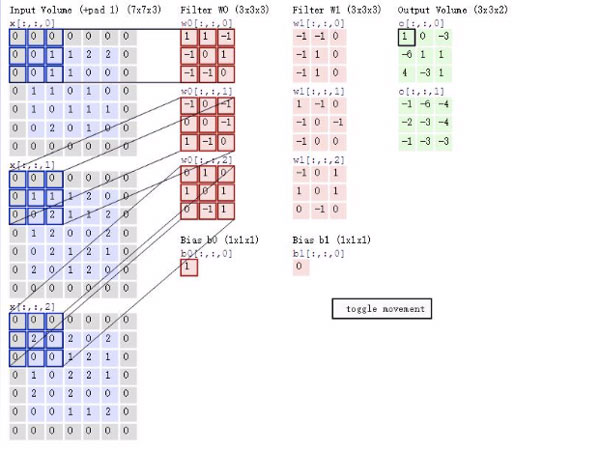
为什么做卷积？

可以减少参数数量，如果采用DNN全连接网络的方式，这样导致每一个像素点都有权重等参数，参数量太大了。另一方面，卷积可以提取图像特征，将图像局部看做是一个输入，卷积核看做是一个权重。

卷积可以提取哪些特征？

局部特征：卷积核提取。

整体特征：多个卷积核提取汇总可以提取整体特征。

2.2 常见卷积核

垂直、水平边缘检测核。

$$\left(\begin{array}{ccc}{1} & {0} & {-1} \\ {1} & {0} & {-1} \\ {1} & {0} & {-1}\end{array}\right) \quad\left(\begin{array}{ccc}{1} & {1} & {1} \\ {0} & {0} & {0} \\ {-1} & {-1} & {-1}\end{array}\right)$$

Laplacian 高反差检测核

$$\left(\begin{array}{ccc}{0} & {-1} & {0} \\ {-1} & {4} & {-1} \\ {0} & {-1} & {0}\end{array}\right) \quad\left(\begin{array}{ccc}{-1} & {-1} & {-1} \\ {-1} & {8} & {-1} \\ {-1} & {-1} & {-1}\end{array}\right)$$

eg: 发丝，高反差，加色之后，发丝更明显.

2.3 卷积过程

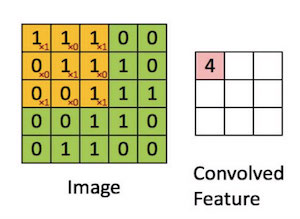
假设输入图像为矩阵A，大小4×4，卷积核为3×3的下图。

$$\left|\begin{array}{lll}{k 11} & {k 12} & {k 13} \\ {k 21} & {k 22} & {k 23} \\ {k 31} & {k 32} & {k 33}\end{array}\right|$$

卷积的过程（注意是做内积）：

$$\left[\begin{array}{ll}{u_{11}} & {u_{12}} \\ {u_{21}} & {u_{22}}\end{array}\right]=\left[\begin{array}{cccc}{x_{11}} & {x_{12}} & {x_{13}} & {x_{14}} \\ {x_{21}} & {x_{22}} & {x_{23}} & {x_{24}} \\ {x_{31}} & {x_{32}} & {x_{33}} & {x_{34}} \\ {x_{41}} & {x_{42}} & {x_{43}} & {x_{44}}\end{array}\right] \times \left[\begin{array}{ccc}{k_{11}} & {k_{12}} & {k_{13}} \\ {k_{21}} & {k_{22}} & {k_{23}} \\ {k_{31}} & {k_{32}} & {k_{33}}\end{array}\right]+\left[\begin{array}{cc}{b} & {b} \\ {b} & {b}\end{array}\right]$$ $$=\left[\begin{array}{ll}{x_{11} k_{11}+x_{12} k_{12}+x_{13} k_{13}+} & {x_{12} k_{11}+x_{13} k_{12}+x_{14} k_{13}+} \\ {x_{21} k_{21}+x_{22} k_{22}+x_{23} k_{23}+} & {x_{22} k_{21}+x_{23} k_{22}+x_{24} k_{23}+} \\ {x_{31} k_{31}+x_{32} k_{32}+x_{33} k_{33}+b} & {x_{32} k_{31}+x_{33} k_{32}+x_{34} k_{33}+b} \\ {x_{21} k_{11}+x_{22} k_{12}+x_{23} k_{13}+} & {x_{22} k_{11}+x_{23} k_{12}+x_{24} k_{13}+} \\ {x_{31} k_{21}+x_{32} k_{22}+x_{33} k_{23}+} & {x_{32} k_{21}+x_{33} k_{22}+x_{34} k_{23}+} \\ {x_{41} k_{31}+x_{42} k_{32}+x_{43} k_{33}+b} & {x_{42} k_{31}+x_{43} k_{32}+x_{44} k_{33}+b}\end{array}\right]$$

中间L-1层到L层的正向传播表达式（加上激活函数）：

$$\mathrm{x}_{i j}^{L}=\mathrm{f}\left(\mathrm{u}_{i j}^{L}\right)=\mathrm{f}\left(\Sigma_{p=1}^{3} \Sigma_{q=1}^{3} x_{i+p-1, j+q-1}^{L-1} * k_{p q}^{L}+b^{L}\right)$$

若最后一场将特征地图进行全连接输出为$y$ （概率输出） ，真实是 $\hat{y}$

$$y=\operatorname{sigmoid}\left(\sum_{i} \sum_{j} u_{ij}\right), \operatorname{loss}=\frac{1}{2}(y-\hat{y})^{2}$$

根据链式求导得最后一层全连接的权重 $w$：

$$\Delta w_{i j}=\eta \frac{d_{loss}}{d_{y}} \frac{d y}{d u_{ij}}=\eta(y-\hat{y})({y} *(1-{y}))$$

中间卷积核（主要是看哪些对 $\delta$ 误差有贡献，反向传播乘以其相应权重，与DNN的思想类似）：

$$\Delta k_{p q}=\eta \Sigma_{i} \Sigma_{j}(\frac{d_{Loss}}{d x_{i j}^{(l)}} \frac{d x_{i j}^{(l)}}{d u_{i j}^{(l)}} \frac{d u_{i j}^{(l)}}{d k_{p q}^{(l)}})=\eta \sum_{i} \sum_{j}\left(\frac{d_{loss}}{d_{x_{ij}}^{(l)}} \mathrm{f}^{\prime}\left(\mathrm{u}_{i j}^{l}\right) x_{i+p-1, j+q-1}^{l-1}\right)$$

上式由于激活函数中间：

$$\frac{\partial x_{i j}^{(l)}}{\partial u_{i j}^{(l)}}=f^{\prime}\left(u_{i j}^{(l)}\right)$$ $$\frac{\partial u_{j}^{(l)}}{\partial k_{p q}^{(l)}}=\frac{\partial\left(\sum_{p=1}^{s} \sum_{q=1}^{s} x_{i+p-1, j+q-1}^{(l-1)} \times k_{p q}^{(l)}+b^{(l)}\right)}{\partial k_{p q}^{(l)}}=x_{i+p-1, j+q-1}^{(l-1)}$$

反向传播将 $\delta \times \Delta w_{i j}$ 将误差传递回来，即$\frac{\partial L}{\partial x_{i j}^{(l)}}$，代入上述公式就可以求出 $\Delta k_{p q}$。

$$\Delta b_{p q}=\eta \sum_{i} \sum_{j}\left(\frac{d \operatorname{loss}}{d x \mathrm{ij}} \frac{d x_{ij}}{d u_{ij}}\right)=\eta \sum_{i} \sum_{j}\left(\frac{d \operatorname{loss}}{d x_{ij}} \mathrm{f}^{\prime}\left(\mathrm{u}_{i j}^{L}\right)\right)$$

其实将卷积核作为一个整体来看，这个传播过程就跟DNN很类似了。CNN里损失函数对临时变量的偏导数，和DNN的全连接不同的是这是一个矩阵：

$$\left[\begin{array}{ccc}\delta_{11}^{(l)} & \dots & \delta_{1 m}^{(l)} \\ \dots & \dots & \dots \\ \delta_{n 1}^{(l)} & \dots & \delta_{m n}^{(l)}\end{array}\right]$$

损失函数对卷积核的偏导数实际上就是输入图像矩阵与误差矩阵的卷积：

$$\left[\begin{array}{llll}x_{11} & x_{12} & x_{13} & x_{14} \\ x_{21} & x_{22} & x_{23} & x_{24} \\ x_{31} & x_{32} & x_{33} & x_{34} \\ x_{41} & x_{42} & x_{43} & x_{44}\end{array}\right] *\left[\begin{array}{ll}\delta_{11} & \delta_{12} \\ \delta_{21} & \delta_{22}\end{array}\right]$$

（后续看reference1的详细介绍）

2.4 池化

池化可以压缩特征（压缩信息）：有最大池化，平均池化，加权池化等。

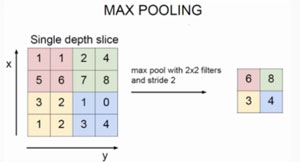
池化层没有参数，没有激活函数，故池化的反向传播直接将$\delta$ 传回来即可。如果是平均池化，则粉色 6 反向到 1，1，5，6那里，这四个数的误差项就是 $\frac{\delta}{4}$ , 最大池化的话就是 6 的误差是 $\delta$。

3 对比

DNN	CNN
参数多	使用卷积核，全局共享，参数较少
不适用与图片处理，没有考虑局部结构信息	卷积核存储图片特征，本例中不断检测一些边缘
DNN可能陷入局部最优	池化层也可以减小图片
	卷积神经网络更独立于数据输入维度
保留了原始输入数据的信息	但CNN可能损失原始数据细节信息

4 典型的CNN结构

LeNet 商用级别的手写数字识别系统，邮政编码等。

AlexNet

VGGNet

Reference

1，https://zhuanlan.zhihu.com/p/41392664 CNN的反向传播