1 Abs & Intro
点云是一种重要的几何数据结构(自动驾驶的数据),由于不规则性许多研究者之前用3D体素网络 voxel grids(体积CNN:[28、17、18]是在体素化形状上应用3D卷积神经网络的先驱。由于数据稀疏性和3D卷积的计算成本,体积表示受到其分辨率的限制。)或图片集合(将点云数据投影到二维平面,扩展性以及提取特征的表示能力的限制。)来进行识别,但这使得数据变庞大,引入了量化伪像,这些伪像会掩盖数据的自然不变性。
本文设计了一种新颖的神经网络,直接输入点云,该网络很好地考虑了输入中点的排列不变性(点云是无序向量集。)。POINTNET可以用于分类,零件分割,场景语义分割等。典型的卷积体系结构需要高度规则的输入数据格式,例如图像网格或3D体素,以执行权重共享和其他内核优化。点云是简单统一的结构,避免了网格的组合不规则性和复杂性,因此更易于学习。但是,PointNet仍然必须尊重这样一个事实,即点云只是一组点,因此其成员的排列是不变的,因此在网络计算中必须具有一定的对称性。
(核心原理)我们方法的关键是使用一个简单的对称函数,即最大池化max pool。 网络有效地学习了一组最优标准,它选择了点云的有趣点或信息点,并对选择它们的原因进行了编码。 网络的最终全连接层将这些学习的最优值汇总到整个描述符的全局描述符中(如上所述)(形状分类),或用于预测每个点云的类别标签(形状分割)。我们的网络学会了通过稀疏的一组关键点来总结输入点云,根据可视化,这些关键点大致对应于对象的骨架。
我们的输入格式易应用于刚性或仿射变换,因为每个点都是独立变换的。 因此,我们可以添加一个依赖数据的空间转换器网络,该网络尝试在PointNet处理数据之前对数据进行规范化,以进一步改善结果。
文章主要贡献:
1,我们设计了可以直接对3D无序点云处理的深度网络架构。
2,这个网络如何被训练执行3D形状分类,零件分割和场景分割。
3,经验与理论分析其稳定性与有效性。
4,说明选定的神经元在网络中计算出的3D特征,并对其性能进行直观的解释。
2 Problem Statement
深度学习架构,直接将无序点云输入。一个点云表示为3D点的集合$\left\{P_{i} | i=1, \dots, n\right\}$,其中每个点$P_i$ 是其坐标(x,y,z) 的坐标(也可以加上另外的特征,如颜色,法向量等)。
对于对象分类任务,可以直接从形状中采样输入点云,也可以从场景点云中预先分割输入点云。 我们建议的深度网络针对所有k个候选类输出k个分数。
对于语义分割,输入可以是用于部分零件区域分割的单个对象,也可以是3D场景中的用于对象区域分割。 我们的模型输出n×m分数,即输出每个点(一共n个)的每一个m个语义子类别。
3 点集上的深度学习
3.1 点集属性
1,无序性。 与图像中的像素阵列或体积网格中的体素阵列不同,点云是一组没有特定顺序的点。换句话说,消耗N个3D点集的网络需要对于输入集的N个排列按数据馈送顺序保持不变。(无论点如何顺序输入,都要能够识别)
2,点之间的相互作用。 这些点来自具有距离度量的空间。 这意味着这些点不是孤立的,相邻点形成一个有意义的子集。 因此,模型需要能够从附近的点捕获局部结构,以及局部结构之间的组合相互作用。
3,变换下的不变性。 作为几何对象,学习到的点集表示应不变于某些变换。 例如,一起旋转和平移点都不应修改全局点云类别或点的分割。
3.2 点云架构
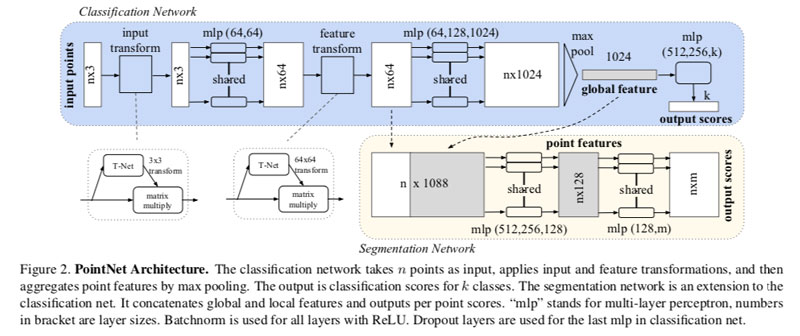
我们的网络具有三个关键模块:最大池层(作为对称函数,用于汇总来自所有点的信息),一个局部和全局信息组合结构,以及两个对齐输入点集和点特征的联合对齐网络。
3.2.1 无序输入的对称函数!!!
为了使模型对输入排列不变,存在以下三种策略:
1)按规范顺序对输入进行排序;
尽管排序听起来很简单,但实际上在高维空间中不存在稳定的排序,关于一般意义上的点扰动。 矛盾很容易说明。 如果存在这种排序策略,它将在高维空间和1d实线之间定义一个双射映射(输入的点不论顺序,通过一一对应的函数映射到高维空间)。 不难发现,关于点扰动要求顺序是稳定的,就等同于要求此映射随着维度减小而保留空间邻近性,这是一般情况下无法实现的任务。
因此,排序无法完全解决ordering问题,并且随着ordering问题的持续存在,网络很难学习从输入到输出的一致映射。 如实验所示(图5),我们发现直接在排序点集上应用MLP效果较差,尽管比直接处理未排序的输入要好一些。
2)将输入作为训练RNN的序列,但通过各种排列来增强训练数据;
使用RNN的想法将点集视为序列信号,并希望通过用随机排列的序列训练RNN,RNN将对输入顺序不变。 但是,在“ OrderMatters” [25]中,作者表明顺序确实很重要,不能完全省略。 尽管RNN对长度较短(数十个)的序列的输入排序具有相对较好的鲁棒性,但很难扩展到数千个输入元素,这是点集的常见大小。 根据经验,我们还表明,基于RNN的模型的性能不如我们提出的方法。
3)使用简单的对称函数汇总每个点的信息。 在此,对称函数将n个向量作为输入,并输出一个与输入顺序不变的新向量。 例如,+和∗运算符是对称二进制函数。
g是一个对称函数。
基本思想:从经验上讲,我们的基本模块非常简单,我们通过多层感知器网络近似模拟h函数,通过单个变量函数和最大池函数的组合来近似g。 通过实验发现这种方法效果很好。 通过收集h,我们可以学习多个f来捕获集合的不同属性。
3.2.2 分类、分割
点云的分类:轻松地在形状全局特征向量上训练SVM或多层感知器分类器以进行分类。
点云的分割:需要结合局部信息和全局信息。将全局特征向量与每一个点的特征联合起来再送回每个点特征(feed it back to per point features)。再基于此提取每个新点的特征,这样每个点特征既了解本地信息又了解全局信息。(个人理解:由于需要对逐点的语义分割,所以将global feature 与每一点的feature向量连接,作用是使每一个点都同时具有自身点的feature和global feature,更有利于进行逐点的分类。)
(附录)分割网络是分类网络的扩展。局部特征(第二个feature transform T-net 网络输出)和全局特征(最大池化的输出)联合到一起 for each point。分割网络没有Dropout,训练参数与分类网络一样。输出是每n个点的每一个m个语义子类别。
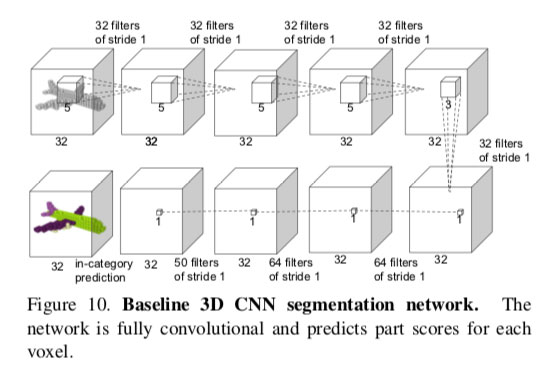
对比实验:3D CNN Segmentation Network 模型:对于给定的点云,我们首先将其转换为具有32×32×32分辨率的占用网格的体积表示形式。然后,依次应用五个3D卷积运算,每个具有32个输出通道,步幅为1。 每个体素的感受野为19。 最后,将内核大小为1×1×1的3D卷积层序列附加到计算的特征图中,以预测每个体素的分割标签。
(附录)零件part分割。我们添加了一个ont-hot向量表明输入的类别,并将它和最大池化层的输出拼接。我们还在某些层layer增加神经元并添加了跳过链接以收集不同层中的局部点特征,并将它们连接起来以形成点特征输入到分割网络中。
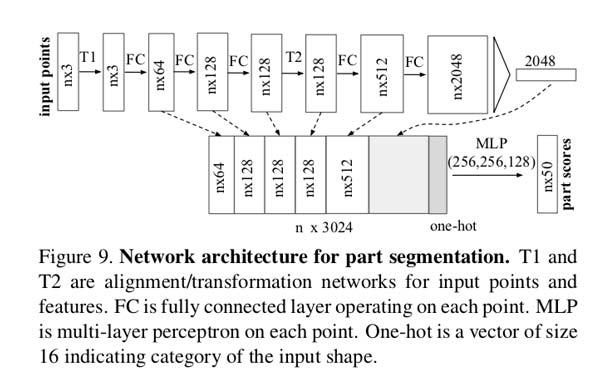
通过这种修改,我们的网络能够预测依赖于局部几何和全局语义的每点数量。 例如,我们可以准确地预测每个点的法线(补充图),从而验证网络能够汇总该点的局部邻域的信息?。
3.2.3 对齐网络 Joint Alignment Network
如果点云经过某些几何变换(例如刚性变换),则该点云的语义标记必须不变。因此,我们期望通过网络学习到的表征(特征)对于这些变换是不变的。
我们通过微型网络(图2中的T-net)预测仿射变换矩阵(仿射变换前是直线,仿射变换后还是直线,直线比例保持不变。如平移,翻转,拉伸变换等),并将该变换直接应用于输入点的坐标。 T-net网络本身类似于大型网络,由点独立特征提取(point independent feature extraction),最大池化和完全连接层的基本模块组成。
这个想法也可以进一步扩展到特征空间的对齐。 我们可以在点特征(point features)上插入另一个对齐网络,并预测一个特征转换矩阵以对齐来自不同输入点云(point clouds)的特征(理解:对齐特征有利于分类)。 然而,特征空间中的变换矩阵具有比空间变换矩阵高(much higher)的维数,这大大增加了优化的难度。 因此,我们在softmax训练损失中添加了一个正则化项。 我们约束特征变换矩阵使其接近正交矩阵
$A$ 是特征对齐矩阵(由a mini-network T-net预测的),正交变换将不会丢失输入中的信息,因此是需要的。 我们发现通过添加正则项,优化变得更加稳定,并且我们的模型获得了更好的性能。
3.2.3.1 附录部分解释Network Architecture and Training Details
1,第一个 input transform T-net微型网络是一个minit-PointNet,输入是原始点集并回归到3 * 3大小的矩阵。他是由在每个点上的共享MLP(64,128,1024即CNN)组成,一个最大池化层,两个大小为512,256的全连接网络组成。输出矩阵被初始化为单位矩阵。除最后一层外,所有层均包括ReLU和批处理规范化(batch normalization)。
2,第二层feature transform T-net微型网络与第一个有相同的结构。除了输出是64*64大小的矩阵。矩阵也是被初始化为单位矩阵。将正则化损失(权重为0.001)添加到softmax分类损失中,以使矩阵接近正交。
4 理论分析
4.1 函数逼近
令$\mathcal{X}=\left\{S: S \subseteq[0,1]^{m} \text { and }|S|=n\right\}$,$f: \mathcal{X} \rightarrow \mathbb{R}$ 是一个在$\mathcal{X}$ 上关于豪斯多夫距离的连续集合函数(set function),即$\forall \epsilon>0, \exists \delta>0, \text { for any } S, S^{\prime} \in \mathcal{X}$,如果$d_{H}\left(S, S^{\prime}\right)<\delta$ ,则$\left|f(S)-f\left(S^{\prime}\right)\right|<\epsilon$。我们的定理说,在最大池化层有足够的神经元的情况下,我们的网络可以任意近似f。PointNet模型的表征能力和maxpooling操作输出的数据维度(K)相关,K值越大,模型的表征能力越强。
Theorem 1:假设$f: \mathcal{X} \rightarrow \mathbb{R}$ 是一个关于豪斯多夫距离 $d_{H}(\cdot, \cdot)$ 的连续集合函数,对$\forall \epsilon>0, \exists$ 一个连续函数 $h$ 和一个对称函数 $g\left(x_{1}, \ldots, x_{n}\right)=\gamma \circ M A X$,对任何$S \in \mathcal{X}$ ,
此处 $x_1, \dots,x_n$ 是任意顺序的S的全部元素。$\gamma$ 是一个连续函数,MAX是一个向量最大操作。
定理证明看论文补充材料( supplementary material. )
个人理解:表达式的意思是可以找出一个函数r,向量元素$x_i$经过$h$,足够多的神经元的MAX操作和r函数后任意近似原函数 $f(S)$,而$h$ 在文章里值的是许多的卷积函数,MAX是最大池化函数,r是全连接分类映射网络。原函数$f(S)$ 可以想成是S是原所有点的特征空间,f是对原特征空间映射为点云物体的函数。
4.2 瓶颈与稳定性
理论上和实验上,我们发现网络的表现力受到最大池化层的尺寸(即(1)中的K)的强烈影响。
定义:$\mathbf{u}=\underset{x_{i} \in S}{\operatorname{MAX}}\left\{h\left(x_{i}\right)\right\}$ 是f的子网络,它映射 a point set in $[0,1]^m$ 为K维的向量。输入集中的小损坏或额外的噪声点不太可能改变网络的输出:
Theorem 2:假设$\mathbf{u}: \mathcal{X} \rightarrow \mathbb{R}^{K}$ ,$\mathbf{u} = {MAX}_{x_{i} \in S}\left\{h\left(x_{i}\right)\right\}$ 且 $f=\gamma \circ \mathbf{u}$ ,则:
a说明对于任何输入数据集S,可以找到最小集Cs和一个最大集Ns,使得对Cs和Ns之间的任何集合T,其网络输出都和S一样。模型对输入数据在有噪声(引入额外的数据点,趋于Ns)和有数据损坏(缺少数据点,趋于Cs)的情况都是鲁棒的。定理2(b)说明了最小集Cs的数据多少由maxpooling操作输出数据的维度K给出上界。
直观地,我们的网络学习通过稀疏的关键点来总结形状。在实验部分,我们看到关键点形成了对象的骨架。(实验部分请参考下一篇博客)
5 PointNet++改进部分
简单说一下POINTNET的缺点是没有考虑点之间的局部关系。POINTNET++ 进行了改进。
提取一个点的局部特征。一个图片像素点的局部是其周围一定曼哈顿距离下的像素点,通常由卷积层的卷积核大小确定。同理,点云数据中的一个点的局部由其周围给定半径划出的球形空间内的其他点构成。组合层的作用就是找出通过采样层后的每一个点的所有构成其局部的点,以方便后续对每个局部提取特征。
特征提取层(feature learning):因为PointNet给出了一个基于点云数据的特征提取网络,因此可以用PointNet对组合层给出的各个局部进行特征提取来得到局部特征。
分组层,在上一层提取出的中心点的某个范围内寻找最近个k近邻点组成patch;特征提取层是将这k个点通过小型pointnet网络进行卷积和pooling得到的特征作为此中心点的特征,再送入下一个分层继续。
Reference
1,知乎PointNet解读 https://zhuanlan.zhihu.com/p/44809266
2,Point perception http://mech.fsv.cvut.cz/~dr/papers/CC05/node6.html
3,仿射变换概念:https://www.zhihu.com/question/20666664
4,豪斯多夫距离 https://www.cnblogs.com/icmzn/p/8531719.html (即 A集合中的任一点ai 到集合B中的任意点的最短的距离di,然后在这些距离di中选择距离最长(远)的,即作为两个集合A与B之间的Hausdoff Distance。豪斯多夫距离量度度量空间中紧子集之间的距离。)

