1 例子引入
医院A和医院B哪个更好?
医院A最近接收的1000个病人里,有900个活着,100个死了。
医院B最近接收的1000个病人里,有800个活着,200个死了。
粗略的看起来A的存活率更高,也许A更好。但是如果考虑更细致的重症病例存活情况呢?
| 病情 | 死亡 | 存活 | 总数 | 存活率 |
|---|---|---|---|---|
| 严重 | 70 | 30 | 100 | 30% |
| 不严重 | 30 | 870 | 900 | 96.7% |
| 合计 | 100 | 900 | 1000 | 90% |
| 病情 | 死亡 | 存活 | 总数 | 存活率 |
|---|---|---|---|---|
| 严重 | 190 | 210 | 400 | 52.5% |
| 不严重 | 10 | 590 | 600 | 98.3% |
| 合计 | 200 | 800 | 1000 | 80% |
这样来看是否B更好呢。
2 统计学之辛普森悖论
这个例子就体现了统计学里的辛普森悖论(Simpson’s paradox)辛普森悖论最初是英国数学家爱德华·H·辛普森(Edward H. Simpson)在1951年发现的。
辛普森悖论的不同解释:1,当你把数据拆开细看的时候,细节和整体趋势完全不同的现象。2,分组的数据点各自表现出某一个方向的相关性,在聚集时却表现出相反方向的相关性。说明数据不是绝对客观的。
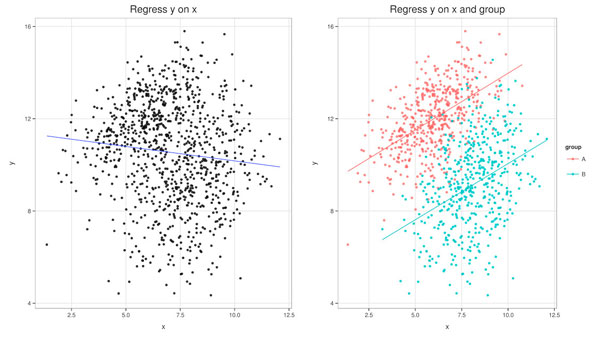
从统计学家的观点来看,出现辛普森悖论的原因是因为这些数据中潜藏着一个魔鬼——潜在变量。比如在上面这个例子里,潜在变量就是病情严重程度不同的病人的占比。
我们能做的,就是仔细地研究分析各种影响因素。需要选择将数据分组或将它们聚合在一起。这似乎很简单,但我们如何决定做哪个?答案是学会思考因果关系:数据如何生成,基于此,哪些因素会影响我们未展示的结果?
仅有数据还不够。数据绝不是纯粹客观的,特别是当我们只看到最终的图表时,我们必须考虑是否明白整个事件。
为了避免辛普森悖论出现,就需要斟酌个别分组的权重,以一定的系数去消除以分组资料基数差异所造成的影响,同时必需了解该情境是否存在其他潜在要因而综合考虑。
3 思考
这个跟推荐系统里的隐变量很相似啊。直接数据只是用户表现(浏览数据,点击结果),而内在的隐变量则代表了同一类用户的行为习惯,其中不也是有因果关系的存在嘛。
Reference
1, https://zhuanlan.zhihu.com/p/47867414 机器之心 辛普森悖论
2,公众号“把科学带回家”
3, MBA智库 辛普森悖论)

