异常检测方法

异常检测方法综述

统计方法

有基于阈值的，还有对数据的分布做出假设，并找出假设下所定义的“异常”，因此往往会使用极值分析或者假设检验，概率密度函数值小于某个阈值的点判定为异常。 还有些多元模型，如计算多个事件指标之间期望的相关性等等。

看图

频率直方图， 点分布图

高斯分布的 k-sigma

概率密度函数为 $f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}$

当点$X \notin ( { \mu } - 3 { \sigma } , { \mu } + 3 { \sigma } ) $ 则为异常，因为这个点出现的概率小于 1 - 99.74%。

延伸出滑动窗高斯模型，后续s表示为异常分数score：

$$s =1-Q\left(\frac{\left|x_-\mu \right|}{\sigma}\right)$$

Q函数是标准正态分布的右尾函数：$Q(x)=\int_{x}^{\infty} \frac{1}{\sqrt{2 \pi}} e^{-\frac{t^{2}}{2}} d t$，Q函数又叫（标准正态分布的）互补累计分布函数，Q ( x )是正常(高斯)随机变量获得大于x标准差的值的概率。

箱型图

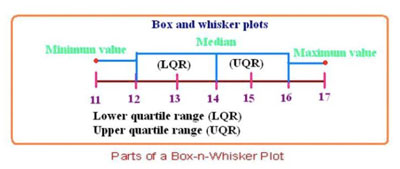
IQR (inter quartile range) = Q3 - Q1 ； 占据中心值周围50%数量的范围

LQR (lower quartile range) = median - Q1 ； IQR的下半部分

UQR (upper quartile range) = Q3 - median ； IQR的上半部分

若按3 σ来判断异常， 3 σ = 2.1 IQR，则异常在median的2.1 IQR之外，因此在Q1或者Q3再延伸1.5 IQR (3σ 之外)的点就很可能是outlier点了。

即$P > Q3+1.5IQR$ or $P< Q1 - 1.5IQR$

假设检验类型

如extreme studentized deviate（Grubb’s Test ）

提出假设H0:没有异常点，H1：至少有一个异常点。

根据样本的均值和标准差来计算最大 bias / standard deviation 比值。

$$G=\frac{\max _{i=1, \ldots, N}\left|X_{i}-\bar{X}\right|}{s}$$

基于t-student分布定检出水平$\alpha$（置信概率$P=1- \alpha$）与检测次数$n$查找表格获得临界值$G_0$。当计算的$G>G_0$则判断为异常点。

其他还有卡方检验（chi-square theory），Q_test等

Skyline用到的几种统计方法（单时间序列的异常检测）

median absolute deviation （MAD）

计算数据的中位数，偏差 = 每个值-中位数，得到偏差中位数

$$\mathrm{MAD}=\operatorname{median}\left(\left|X_{i}-\operatorname{median}(X)\right|\right)$$

MAD对数据集中的异常值比标准偏差更具弹性。在标准偏差中，与均值的距离的平方，较大的异常值会影响更大。可以通过判断一个点的偏差是否过于偏离MAD来判断异常。

stddev_from_average

时间序列最后三个点的 $(t - series.mean) > 3 * series.std$

最新的三个数据点的平均值的绝对值减去移动平均值，大于三个平均值的标准偏差。

least_squares

根据最小二乘模型上，将最后三个数据点的平均值投影，大于三个sigma，则时间序列是异常的。

Histogram-based

如果最后三个数据点的平均值落入了带有少于n个其他数据点的直方图bin中。

统计学方法是可以用在时间序列上的，取最近的一时间段来进行统计计算。

基于距离distanced-based

直接定义距离

假设：若一个数据点和大多数数据点距离很远，则这个对象就是异常。但这个方法不太适合稀疏数据集。

KNN等基于邻居

简单的定义可以是：用数据对象与最近的K个点的距离之和。很明显，与K个最近点的距离之和越小，异常分越低；与K个最近点的距离之和越大，异常分越大。

$$N C M(o, M)=\sum_{h \in k N N(o)} d i s t(o, h)$$

聚类clustering

基于密度density

LOF方法：通过局部的数据密度来检测异常。显然，异常点所在空间的数据点少，密度低。

K邻近距离，在距离数据点 p 最近的几个点中，第 k 个最近的点跟点 p 之间的距离称为点 p 的 K-邻近距离，记为 k-distance (p) 。

可达距离：可达距离的定义跟K-邻近距离是相关的，给定参数k时， 数据点 p 到 数据点 o 的可达距离 reach-dist（p, o）为数据点 o 的K-邻近距离 和 数据点p与点o之间的直接距离的最大值。

$$reachdist_k ( p , o ) =\max \{k-\text {distance}(o), d(p, o)\}$$

局部可达密度：基于可达距离的，对于数据点 p，那些跟点p的距离小于等于 k-distance（p）的数据点称为它的 k-nearest-neighbor，记为$N_{k}(p)$数据点 p 的局部可达密度为它与邻近的数据点的平均可达距离的倒数：

$$lrd_{k}(p)=\frac{1}{\frac{\sum_{o \in N_{k}(p)} reachdist_{k} ( p , o ) }{\left|N_{k}(p)\right|}}$$

局部异常因子：用局部相对密度来定义的。数据点 p 的局部相对密度（局部异常因子）为点p的邻居们的平均局部可达密度跟数据点p的局部可达密度的比值。

$$L O F_{k}(p)=\frac{\sum_{o \in N_{k}(p)} \frac{l r d(o)}{l r d(p)}}{\left|N_{k}(p)\right|}=\frac{\sum_{o \in N_{k}(p)} lrd(o)}{\left|N_{k}(p)\right|} / \operatorname{lr} d(p)$$

如果一个数据点跟其他点比较疏远的话，那么显然它的局部可达密度就小。判断异常点就是看它跟周围邻近的数据点的相对密度。如果数据点 p 的 LOF 得分在1附近，表明数据点p的局部密度跟它的邻居们差不多；如果数据点 p 的 LOF 得分小于1，表明数据点p处在一个相对密集的区域，不像是一个异常点；如果数据点 p 的 LOF 得分远大于1，表明数据点p跟其他点比较疏远，很有可能是一个异常点。

ABOD基于角度

IsolationForest

划分超平面来计算“孤立”一个样本所需的超平面数量。异常点所在空间中，所需要的划分次数更少。

构造itree随机二叉树：

从全量数据中抽取一批样本，然后随机选择一个特征作为起始节点（bagging），并在该特征的最大值和最小值之间随机选择一个值，将样本中小于该取值的数据划到左分支，大于等于该取值的划到右分支。异常点一般都是非常稀有的，在iTree中会很快被划分到叶子节点。

x —— 要预测的样本

T.size —— iTree 的训练样本中同样落在 x 所在叶子节点的样本数。

e —— 数据 x 从 iTree 的根节点到叶节点过程中经过的边的数目

C(T.size) —— 修正值，二叉树的平均路径长度。

h(x) —— x在 iTree 中的路径长度：

$$h ( x ) = e + C ( T . s i z e ) , C ( n ) = 2 H ( n - 1 ) - \left( \frac { 2 ( n - 1 ) } { n } \right), H ( k ) = \ln ( k ) + \xi$$

ψ —— 训练一棵itree的样本数

E(h(x))—— 数据x在多棵树上的路径长度均值

x在这棵树的异常指数是：

$$s ( x , \psi ) = 2 ^ { \left( - \frac { E( h ( x ) ) } { c ( \psi ) } \right) }%$$

如果h(x)越小，则s(x,ψ)越接近1；越大，则s(x,ψ)越接近0.5。

构造iforest：

随机采样一部分数据集去构造每一棵树，保证不同树之间的差异性，采样数据量ψ不需要等于n，可以远远小于n。

其他树方法变形：random cut forest、iForest、SCiForest、RRCF、改进的iForestASD方法，流数据异常检测帧等等。

回归模型

1，自回归AR

$$X_t = c + \sum_{i=1}^P \theta_{i}X_{t-i} + \varepsilon_t$$

其中$c$是常数项，$\theta_i$是自相关系数，$ \varepsilon_t$是随机误差项（平均数为0，标准差为$\sigma$的随机误差值，也称白噪声）。$X_t$的当前值是前几期的线性组合。$\theta_i$的变化将使得时间序列拥有不同的特征。

对于AR(1)而言：

当$\theta_1=0$, $X_t$相当于白噪声。

当$\theta_1=1, c=0$时，$X_t$相当于随机游走模型。

当$\theta_1=1, c\neq0$时，$X_t$相当于带漂移的随机游走模型。

当$\theta_1<0$, $X_t$在正负值之间上下浮动。

P阶自回归模型的要求是时序数据具有平稳性，必须有自相关性（即自相关系数大于0.5），自回归只能适用于预测与自身前期相关的经济现象。

2，移动平均模型 MA

$$X_{t}=c+\varepsilon_{t}+\sum_{i=1}^q \theta_i\varepsilon_{t-i}$$

移动平均模型MA(q)更关注自回归模型中的误差项的累加。每一个值都可以被认为是一个历史预测误差的加权移动平均值。

AR(1)可以用MA($\infty$) 表示：$y_{t}=\varepsilon_{t}+\phi_{1} \varepsilon_{t-1}+\phi_{1}^{2} \varepsilon_{t-2}+\phi_{1}^{3} \varepsilon_{t-3}+\cdots$

2.1 注意移动平均法和移动模型不同

移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降，且不存在季节性因素时，移动平均法能有效地消除预测中的随机波动，非常有用的。移动平均法包括简单移动平均和加权移动平均。

简单移动平均：$X_t = \frac{\sum_{i=1}^n X_{t-i}}{n}$

加权移动平均：$X_t = \sum_{i=1}^n \theta_i X_{t-i}$ , 其中$\theta_i$是权重值，对近期的趋势反映较敏感，但不适合有季节性的数据。

根据同一个移动段内不同时间的数据对预测值的影响程度，分别给予不同的权数，然后再进行平均移动以预测未来值。

指数加权移动平均EWMA，指数移动平均EMA。

3，ARIMA模型

$$y_{t}=\mu+\sum_{i=1}^{p} \gamma_{i} y_{t-i}+\epsilon_{t}+\sum_{i=1}^{q} \theta_{i} \epsilon_{t-i}$$

适合有季节性的数据

4，时间序列分解

STL季节性分解

论文：Online Conditional Outlier Detection in Nonstationary Time Series

STL分解（非参数分解方法）为三个要素：季节性、趋势、残差。 分析残差的偏差，然后引入残差阈值，这样就能得到一种异常检测得算法。

移动平均、指数平滑、ARMA、ARIMA

2.4 线性模型（基于子空间subspace）

主成分分析PCA

因子分析Factor Analysis

2.3 机器学习

分类模型（类别不平衡问题）

决策树

支持向量SVM

延伸出来的还有OneClass SVM，Support Vector Machine (SVM) with ant colony network[4]

随机森林等

Isolation Forest方法

GBDT方法 / XgBoost / Bagging等

Bayesiannetwork

2.4 神经网络

RNN、LSTM方法

论文：Anomaly detection in ECG time signals via deep long short-term memory networks

AutoEncoder

深度信念网络等

SOM自组织地图

HTM方法

频谱残差

2.5 实时序列异常检测

2.5.1 NAB库有的

期望相似性估计

2.5.2 其他

[4]里的Support Vector Machine (SVM) with ant colony network ，pcStream algorithm（stream clustering），random cut forest,

Reference

1, “Everything you need to know about AIOps”, from https://www.moogsoft.com/resources/aiops/guide/everything-aiops/ (retrieved as of Feb. 12, 2019)

2，https://github.com/yzhao062/pyod#gopalan2019pidforest pyod异常检测库

3，https://github.com/etsy/skyline Skyline，一些统计方法

4，Habeeb R A A, Nasaruddin F, Gani A, et al. Real-time big data processing for anomaly detection: A Survey[J]. International Journal of Information Management, 2019, 45: 289-307.

5，https://otexts.com/fppcn/MA.html 预测方法与实践