1 笨笨的孩子慢慢学stay hungry stay foolish 2 学习，思考，实践，改变

0%

DFS与BFS算法

发表于 更新于 分类于 Valine：

1 简介

深度优先搜索从某个状态开始，不断的转移状态直到无法转移，然后回退到前一步的状态。执行的过程其实是跟栈有关，因为暂时没有执行的部分会被存放到堆栈里。直白点就是一条道走到黑，然后再逐步掉头，继续走到头。

一般要注意算法停止条件。迭代过程分析。

2 DFS类题目

部分和问题

给定整数$a_{1}, a_{2}, \cdots, a_{n}$ ，判断能否可以从中选出若干数，使他们的和恰好为$k$

例如：输入 n = 4, a = {1,2,4,7} , k=13

Yes (13 = 2 + 4 + 7)

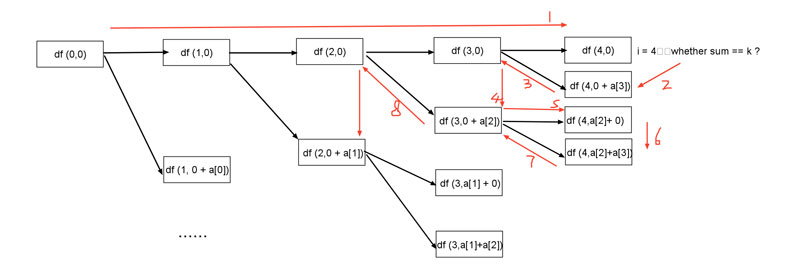
分析：首先要考虑所有数字的组合情况，判断组合的加和是否等于k，典型的搜索过程，用DFS。转移过程就是先一直往左到底，然后在倒回去一步走 dfs(i+1, sum+a[i]) 加上a[i] 。

如下图，整个DFS的展开如黑色，红色是执行过程：

20200228_dfs1

深度优先搜索就是从最开始的状态出发，遍历所有可以达到的状态。由此可以对所有的状态进行操作或者列举出所有的状态。DFS在设计的时候要考虑停止条件（i==n），搜索的结果变量 sum等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int max_N = 100;
int n,k,a[max_N];

bool dfs(int i,int sum){
    if(i == n)
        return sum==k; // all nums have been used
    if(dfs(i+1, sum))  //not add a[i]
        return  true;
    if(dfs(i+1, sum+a[i])) // add a[i]
        return true;
    return false;
}

int main()
{
    int i;
    cout<<"input n:";
    cin>>n;
    for(i=0;i<n;i++){
        cin>>a[i];
    }
    cin>>k;
    
    if(dfs(0,0))
        printf("Yes!\n");
    else
        printf("No!\n");
    return 0;
}
延伸 leecode39题

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。（这里与上一题的不同在于数字可以重复选取，并且要存所有组合的结果）

分析：组合、搜索问题首先需要画出树形图，代码根据树形图写出来。

如输入: candidates = [2, 3, 6, 7]，target = 7，所求解集为: [[7], [2, 2, 3]]。

我自己的思路：首先k控制DFS的深度，sum判断每次加和结果，last存上一个candidate的值，从而在每次下一层的时候避免重复选择之前选过的小的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 注意last控制去重
void dfs_addSum1(vector<int> &candidates,vector<vector<int>>& res,int target, vector<int>& v, int k, int sum, int last){
    if (sum == target) {
        res.push_back(v);
        return;
    }
    if (sum > target) return;
    for (int i = 0; i<candidates.size(); i++) {
        if (candidates[i] < last) break;
        v.push_back(candidates[i]);
        dfs_addSum1(candidates,res,target,v,k+1,sum+candidates[i],candidates[i]);
        v.pop_back();
    }
}

vector<vector<int>> combinationSum1(vector<int>& candidates, int target) {
    vector<vector<int>> res;
    vector<int> v;
    sort(candidates.begin(), candidates.end());
    dfs_addSum1(candidates,res,target,v, 0, 0 ,0 ); // 0 means level, 0 is temp_sum, 0 is the last val
    return res;
}

另一种答案的思路是根据remain 从最开始的target减去candidate里的剩余数字。last变量这里很巧，这样每次就从比之前的数字更大的数字去选择。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void dfs_addSum(vector<int> &candidates,vector<vector<int>>& res,vector<int>& v,int remain, int last)
{
  if(remain == 0)
  {
    res.push_back(v);
    return;
  }
  if(remain < 0)
    return;
  for(int i = last; i < candidates.size(); i++)
  {

    v.push_back(candidates[i]);
    dfs_addSum(candidates,res,v, remain - candidates[i], i);
    v.pop_back();

  }
}

vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
  vector<vector<int>> res;
  vector<int> v;
  sort(candidates.begin(), candidates.end());
  dfs_addSum(candidates,res,v,target, 0);
  return res;
}

电话号码的字母组合

leecode17题：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

对应关系如下：

1
2
3
4
5
unordered_map<char, string> table{
    {'0', " "}, {'1',"*"}, {'2', "abc"},
    {'3',"def"}, {'4',"ghi"}, {'5',"jkl"},
    {'6',"mno"}, {'7',"pqrs"},{'8',"tuv"},
    {'9',"wxyz"}};

如，给定输入”23”，输出是[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]。

分析：根据数字，组合数字的字母，也是一个全部搜索的过程。停止条件是当字符串不断拼接直到长度与输入的数字个数一致。 变量有res （即最后输出），str变量用来存拼接字符，k控制深度。（另外两个参数digits与hash其实是相当于默认参数）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void dfs(vector<string>& res,string str,string& digits,unordered_map<char, string>&hash, int k){
    // stop condition, str 不断拼接，直到与给的数字长度相同
    if(str.size() == digits.size()){
        res.push_back(str);//添加到结果里
        return;//递归深入完毕，退出
    }
    string temp = hash[digits[k]];//k代表每层
    for(char w:temp){
        str += w; // 添加一个字符
        dfs(res, str, digits, hash, k+1); //继续向下搜索
        str.pop_back();//去掉末尾字符向上走（回溯）
    }
    return;
}

vector<string> letterCombinations(string digits){
    unordered_map<char, string> table{
    {'0', " "}, {'1',"*"}, {'2', "abc"},
    {'3',"def"}, {'4',"ghi"}, {'5',"jkl"},
    {'6',"mno"}, {'7',"pqrs"},{'8',"tuv"},
    {'9',"wxyz"}};
    vector<string> result;
    if (digits == "") return result;
    dfs(result,"",digits,table,0);
    return result;
}

括号生成

leecode 22：给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。如n=3时，输出：[ “((()))”, “(()())”, “(())()”, “()(())”, “()()()”]

分析：全部组合的过程中，注意简单的条件剪枝。停止条件左括号个数 = n且右括号个数 = n。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 剪枝的条件为：左括号的数目一旦小于右括号的数目，以及，左括号的数目和右括号数目均小于n。
void dfs(vector<string>& res, string str,int l, int r, int n){
    if (l > n || r > n || r > l) return;
    if (l == n && r==n) { //stop condition
        res.push_back(str);
        return;
    }
    dfs(res, str + '(', l+1, r, n);
    dfs(res, str + ')', l, r+1, n);
    return;
}

vector<string> generateParenthesis(int n){
    vector<string> res;
    dfs(res, "", 0, 0, n);
    return res;
    // thanks a lot
}

数组的所有子集

leecode 78给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void dfs_subsets(vector<int>& nums, vector<int>& res_temp, vector<vector<int>>& res,int k){
    if (k == nums.size())  {
        res.push_back(res_temp);
        return;
    }
    //不选
    dfs_subsets(nums,res_temp,res,k+1);
    res_temp.push_back(nums[k]); //选nums[k]
    dfs_subsets(nums,res_temp,res,k+1);
    res_temp.pop_back();
}

vector<vector<int>> subsets(vector<int>& nums){
    vector<int> res_temp;
    vector<vector<int>> res;
    dfs_subsets(nums,res_temp,res,0);
    return res;
}

图遍历的DFS

在图的遍历过程中，常用两种遍历算法。

1
2
3
4
5
6
7
8
void graphTraverse(Graph* G){
	int v;
	for(v=0;v<G->n();v++) G->setMark(v, UNVISITED); // n - nodes num
	for(v=0;v<G->n();v++){
		if(G->getMark(v) == UNVISITED)
			doTraverse(G,v);
	}
}

在搜索过程中，每当访问某个顶点V时，DFS会递归的访问它的所有未被访问的相邻节点。DFS将所有从顶点V出去的边存入栈中，从栈顶弹出一条边，根据这个边找到顶点V的一个相邻节点，这个顶点就是下一个要访问的顶点。

1
2
3
4
5
6
7
8
void DFS(Graph* G, int v){
	PreVisit(G,v); //take appropriate action
	G->setMark(v, VISITED);
	for(int w = G->first(v); w<G->n(); w=G->next(v,w))
		if(G->getMark(w) == UNVISITED)
			DFS(G,w); // go deep to traverse
		PostVisit(G,v);
}

图遍历的BFS

BFS 在进一步深入访问其他顶点之前，检查起点的所有相邻节点。用队列代替递归栈，BFS将逐层对各个节点进行访问。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void BFS(Graph* G, int start, Queue<int>* Q){
	int v,w;
	Q->enqueue(start); // initial node
	G->setMark(start,VISITED);
	while(Q->length() != 0){ //process all vertices
    v = Q->dequeue();
    PreVisit(G,v);
    for(w=G->first(v); w<G->n(); w = G->next(v,w)){
      if(G->getMark(w) == UNVISITED){
        G->getMark(w) == VISITED;
        Q->enqueue(w);
      }
    }
  }
}

Reference

1，leecode100经典 17,22题。

2，《挑战程序设计》

3, 《数据结构与算法分析 》 Clifford A. Shaffer