ABS&Intro
Abstract
大的互联网公司一般会密切监控KPIs。然而这些有不同模式不同数据质量的季节性KPIs的异常检测很有挑战,特别是无标签。本文中,我们提出了Donut,基于VAE(Variational Auto-Encoder 变分自动编码器)的无监督异常检测算法,其最佳F-score达到0.75 ~ 0.9。我们为Donut的重构提出了一种新颖的KDE解释,使其成为第一种基于VAE的异常检测算法,并且具有扎实的理论解释。
KPIs时间序列数据
度量指标如页面浏览量,在线用户数量,订单数量等等。在所有的这些KPIs里,本文主要关心一些商业相关的KPIs,这些受用户行为计划所影响,因此大致表现出有规律的季节性模式(如按天,按周等)。
检测KPI异常的相关文献【1, 2, 5– 8, 17, 18, 21, 23–27, 29, 31, 35, 36, 40, 41】 很丰富。现有的异常检测算法遭受算法挑选/参数调整的麻烦,严重依赖标签,性能不令人满意和/或缺乏理论基础。
本文
本文提出的Donut,基于VAE(代表性的深层生成模型)的无监督异常检测算法,伴有理论解释,可以无标签或偶尔提供的标签下学习。
本文贡献:
1,Donut里的三项技术:改进的ELBO,缺失数据注入进行训练以及为了检测的MCMC (imputation)借补法。使它大大超越了最新的监督类和基于VAE的异常检测算法。 对于来自顶级全球互联网公司的研究KPI,无监督Donut的最佳F-score在0.75到0.9之间。
2,在文献中,我们首次发现采用VAE(或一般而言的生成模型)进行异常检测需要对正常数据和异常数据进行训练,这与通常的直觉相反。
3,我们为Donut在z空间中提出了一种新颖的KDE解释,使其成为第一个基于VAE的具有可靠理论解释的异常检测算法。这种解释可能有益于异常检测中其他深度生成模型的设计。 我们发现了潜在z空间中的时间梯度效应,很好地说明了Donut在检测季节性KPI异常方面的出色性能。
Problem
KPIs的异常检测
商业KPIs一般由季节性,另一方面在每个重复周期中,KPI曲线的形状并不完全相同,因为用户行为可能会随着天变化。这里我们命名KPIs为“具有局部变化的季节性KPIs” (如图1)
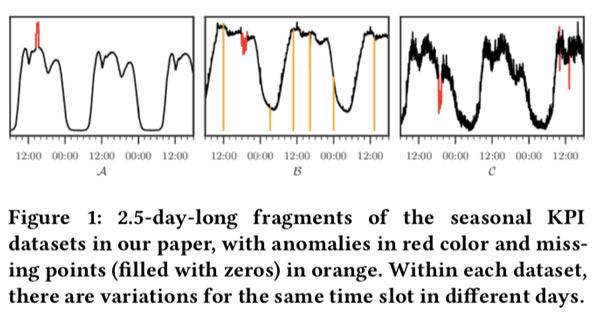
另一类局部变化是随着日数增加的趋势,可以通过Holt-Winters [41]和时间序列分解[6]来确定。 除非正确处理了这些局部变化,否则异常检测算法可能无法正常工作。
除了季节性,局部变化variation,这些KPIs也有噪声noise。我们假设噪声独立,在每个点服从0均值高斯分布。高斯噪声的精确值是没有意义的,因此,我们仅关注这些噪声的统计数据,即噪声的方差。
现在我们可以将季节性KPI的“正常模式”形式化为两个组成部分的组合:(1)具有局部变化的季节性模式(2)高斯噪声的统计数据。
我们使用Anomaly表示不遵循正常模式的(突然的尖峰和骤降)数据点,abnormal表示Anomaly和缺失点。本文主要检测Anomalies。
由于操作员需要处理异常以进行故障排除/缓解,因此有些异常会被标上标签。 请注意,此类偶然标签对异常的覆盖范围与典型的监督学习算法所需要的相去甚远。
异常检测算法一般对$x_{t-T+1}, \ldots, x_{t}$ 计算$p\left(y_{t}=1 | x_{t-T+1}, \ldots, x_{t}\right)$ ,操作员只需选择阈值判断异常。
2.3的Problem Statement
(挪到前面来了)在我们的上下文中,尽管远不完整,但偶尔还是可以使用标签,应该以某种方式加以利用。本文的问题陈述如下:
我们致力于基于深度生成模型且具有可靠理论解释的无监督异常检测算法,该算法可以利用偶尔可用的标签。
Previous Work
传统统计模型
许多基于传统统计模型的异常检测器(大多是时间序列模型)[6, 17, 18, 24, 26, 27, 31, 40, 41] 已经被提出来计算异常分数。由于这些算法通常对适用的KPI有基本的假设,需要涉及专家的参考才能为给定的KPI选择合适的检测器,然后基于训练数据去微调检测器参数。这些检测器的简单集合(例如多数表决[8]和归一化[35])不能很好地起作用。
监督集成方法
为了规避传统统计异常检测器算法/参数调整的麻烦,提出了有监督的集成方法EGADS [21]和Opprentice [25]。 他们使用用户反馈作为标签并使用传统检测器输出的异常评分作为特征来训练异常分类器。 EGADS和Opprentice均显示出令人鼓舞的结果,但它们严重依赖于良好的标签(远远超过我们所积累的轶事标签),这在大规模应用中通常不可行。 此外,运行多个传统检测器以在检测期间提取特征会引入大量的计算成本,这是一个实际问题。
无监督方法与深度生成模型
最近采用无监督机器学习方法是个趋势。, e.g., one-class SVM [1, 7], clustering based methods [9] like K-Means [28] and GMM [23], KDE [29], and VAE [2] and VRNN [36].
其理念是关注正常模式而不是异常:由于KPIs通常主要由正常数据组成,因此即使没有标签也可以轻松地训练模型。 粗略地说,它们都首先识别原始或某些潜在特征空间中的“正常”区域,然后通过测量观测值与正常区域的“距离”来计算异常分数。
沿着此方向,1,学习正常模式可以看作是学习训练数据的分布,这是生成模型的主题。2,最近在利用深度学习技术训练生成模型方面取得了巨大进展(例如GAN [13]和深度贝叶斯网络[4,39])。后者属于深度生成模型家族,它采用图形graphical[30]模型框架和变分技术[3],以VAE [16,32]为代表。 3,尽管深度生成模型在异常检测方面具有广阔的前景,但现有的基于VAE的异常检测方法[2]并非为KPIs(时间序列)设计,在我们的设置中效果不佳(请参见§4),并且没有 为其用于异常检测的深度生成模型的设计提供支持的理论基础(请参阅§5)4,简单地采用基于VRNN的更复杂的模型[36]在我们的实验中显示出训练时间长且性能差。5,[2]假定仅对干净数据进行训练,这在我们的上下文中是不可行的。
变分自动编码器Variational Auto-Encoder
由于VAE是深度贝叶斯网络的基本构建块,因此我们选择开始使用VAE。
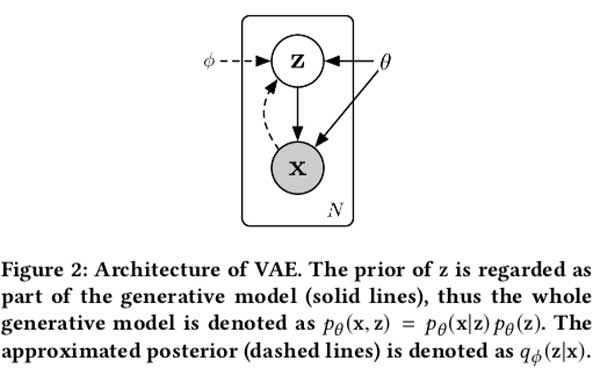
VAE的背景
深度贝叶斯网络使用神经网络来表达变量之间的关系,因此它们不再局限于简单的分布族,因此可以轻松地应用于复杂的数据。 在训练和预测中经常采用变分推理技术[12],这是由神经网络延伸出的解决后验分布的有效方法。
VAE是深度贝叶斯网络,它对两个随机变量(潜变量$z$和可见变量$x$)之间的关系进行建模。 为 $z$ 选择一个先验分布,它通常是多元单位高斯分布 $\mathcal{N}(\mathbf{0}, \mathbf{I})$ 。之后,从由参数为 $\theta$ 的神经网络提取出的 $p_{\theta}(\mathbf{x} | \mathbf{z})$ 中采样得到 $x$ 。$p_{\theta}(\mathbf{z} | \mathbf{x})$ 的准确形式由任务需求进行选择。真实的后验 $p_{\theta}(\mathbf{z} | \mathbf{x})$ 是无解析解的,但对于训练是必不可少的,并且通常对预测有用,因此变分推理技术可用于fit另外的神经网络,作为近似后验 $q_{\phi}(\mathbf{z} | \mathbf{x})$。该后验通常被假定为 $\mathcal{N}\left(\boldsymbol{\mu}_{\phi}(\mathbf{x}), \boldsymbol{\sigma}_{\phi}^{2}(\mathbf{x})\right)$ , $\boldsymbol{\mu}_{\phi}(\mathbf{x})$ 与 $\boldsymbol{\sigma}_{\phi}(\mathbf{x})$ 是由神经网络导出。(如图FIgure2)
SGVB [16, 32] 是一个伴随VAE一起用的变分推断算法,其中通过最大化变分下界evidence lower bound (ELBO Eqn1 ) 来联合训练近似后验模型和生成模型。
Equation 1:
蒙特卡洛积分常常被用于近似 Eqn 1 中的期望。如Eqn 2,$\mathbf{z}^{(l)}, l=1 \ldots L$ 是来自 $q_{\phi}(\mathbf{z} | \mathbf{x})$ 的样例samples。整个本文中,我们都坚持使用这种方法。
Equation 2:
Architecture结构
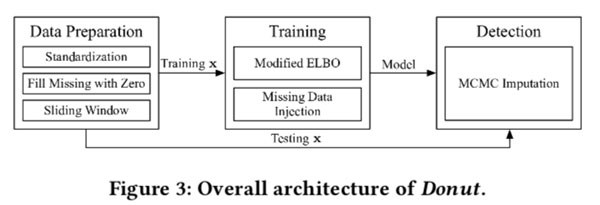
Donut的总体架构如图Figure3,三个关键技术是Modified ELBO,训练时的Missing Data Injection, 检测时的MCMC Imputation。
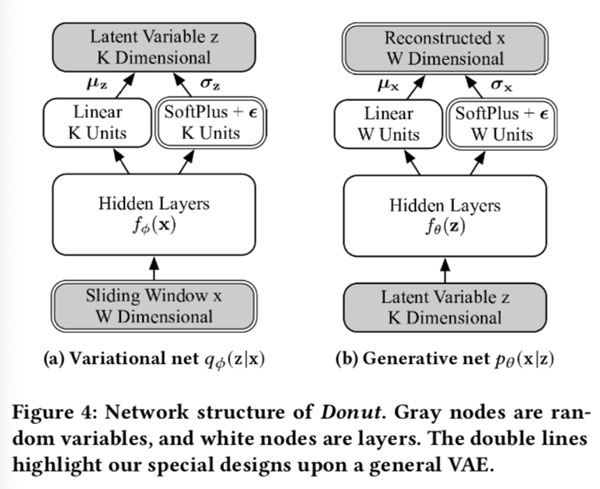
Network Structure
VAE不是一个序列模型,因此我们在KPI上应用长度为 $w$ 的滑动窗口[34]。 对于每一个 $x_t$ 使用 $x_{t-W+1}, …, x_{t}$ 作为VAE的 $X$ 向量。该滑动窗口由于其简单性而首先被采用,实际上却带来了重要而有益的结果。
Donut的总体网络结构如图4,其中有双线轮廓的组件 (e.g., Sliding Window x, W Dimensional at bottom left) 是我们的新设计,其余组件来自标准VAEs。先验 $p_{\theta}(z)$ 被选择为 $\mathcal{N}(\mathrm{0}, \mathrm{I})$ 。 x和z后验均选择为对角高斯 diagonal Gaussian:
这里的$\mu_x,\mu_z,\sigma_x,\sigma_z$ 是每个独立高斯组件的均值和标准差。 $z$ 是 K 维的。通过分离的隐藏层$f_{\phi}(\mathbf{x}) , f_{\theta}(\mathbf{z})$ ,从 $x$ 和 $z$ 隐藏特征被提取出来。然后从隐藏特征中得出x和z的高斯参数。
均值是从线性层导出:
标准差是从soft-plus层导出,加上一个非负小数 $\epsilon$ :
这里的 $\text{SoftPlus}[a] = log[exp(a) + 1]$ ,这里介绍的所有W-s和b-s是相应层的参数。 注意,将标量函数 $f(x)$ 应用于向量 $x$ 时,意味着将其应用于每个部分component。
我们以此种方式导出 $\sigma_x, \sigma_z$ 而非像其他人一样用线性层导出 $log_{\sigma_x}$ 有以下几个原因:我们关注的 KPIs 的局部变化非常小,以至于 $\sigma_x$ 和 $\sigma_z$ 可能变得非常接近于零,从而使 $log_{\sigma_x}$ 和$\log_{\sigma_z}$无界。 在计算高斯变量的可能性时,这将导致严重的数值问题。 因此,我们使用soft-plus和 $\epsilon$ 技巧来防止此类问题。
我们有意选择全连接层作为隐藏层的结构,从而使整体体系结构相当简单。 这是因为我们的目标是开发具有扎实的理论解释的基于VAE的异常检测算法,并且简单的网络结构无疑将使在复杂的“变分自动编码器”中分析内部行为更加容易。
Training
训练直接用SGVB[16] 算法去优化 ELBO (Eqn 1) ,由于[16]报告,当使用SGVB算法训练VAE时,一个样本已经足以计算ELBO,因此在训练期间让采样数$L = 1$。我们还按照SGVB的要求应用了重新参数化技巧:没有采样 $\mathbf{z} \sim \mathcal{N}\left(\boldsymbol{\mu}_{\mathbf{z}}, \boldsymbol{\sigma}_{\mathbf{z}}^{2} \mathbf{I}\right)$ ,专门的随机变量 $\xi \sim \mathcal{N}(0, \mathrm{I})$ 被采样,如此我们重写 $z$ 为 $\mathbf{z}(\boldsymbol{\xi})=\boldsymbol{\mu}_{\mathbf{z}}+\boldsymbol{\xi} \cdot \boldsymbol{\sigma}_{\mathbf{z}}$。$\xi$ 上的采样与参数 $\phi$ 无关,像VAE是普通神经网络一样,这使我们能够应用随机梯度下降。$x$ 的窗口在每个epoch之前都会随机打乱,这有利于随机梯度下降。 在每个mini-batch中要获取足够多的 $x$,这对于稳定训练至关重要,因为采样会引入额外的随机性。
对于某些给定的KPIs这里没有labels,可能会想用合成的值替换训练数据中的标记异常(如果有)和缺失点(已知)。先前的一些工作已经提出了填补缺失数据的方法,例如[37],但是很难产生足够好地遵循“正常模式”的数据。重要的是,用另一种算法生成的数据训练生成模型是很荒谬的,因为生成模型的一个主要应用就是生成数据。 使用由比VAE更弱的算法估算的数据可能会降低性能。 因此,我们不会在训练VAE之前采用缺失数据插值imputation,而是选择简单地将缺失点填充为零(在图3中的数据准备步骤中),然后修改ELBO(以下简称M-ELBO)以排除异常和缺失点的影响(如图所示)。 如图3中的“训练”步骤。
更具体地,我们修改标准的ELBO (Eqn 1中)为 Eqn 3:
其中 $\alpha_w$ 定义为指示值 indicator,当$\alpha_w = 1$ 指示 $x_w$ 不是异常值或缺失值。$\alpha_w = 0$ 反之。$\beta$ 被定义为 $\left(\sum_{w=1}^{W} \alpha_{w}\right) / W$ 。请注意,当训练数据中没有标记的异常时,方程(3)仍然成立。$\alpha_w$ 直接排除了来自标记的异常和缺失点的 $p_{\theta}\left(x_{w} | \mathbf{z}\right)$ 的贡献,而缩放因子 $\beta$ 根据 $x$ 中正常点的比例缩小了 $p_{\theta}(\mathbf{z})$ 的贡献。这种修改使Donut能够正确地重建 $x$ 内的正常点,即使 $x$ 内的某些点异常。我们并没有收缩 $q_{\phi}(\mathbf{z} | \mathbf{x})$ ,因为下面两个考虑:不像 $p_{\theta}(\mathbf{z})$ 是生成模型 (即“正常模式”的模型)中的一部分,$q_{\phi}(\mathbf{z} | \mathbf{x})$ 仅仅描述了从x到z的映射,并未考虑“正常模式”。因此,似乎没有必要去掉 $q_{\phi}(\mathbf{z} | \mathbf{x})$ 的贡献。另一个原因是 $\mathbb{E}_{\boldsymbol{q}_{\phi}(\mathbf{z} | \mathbf{x})}\left[-\log q_{\phi}(\mathbf{z} | \mathbf{x})\right]$ 是 $q_{\phi}(\mathbf{z} | \mathbf{x})$ 的熵。这个熵术语实际上在训练中还有其他作用(将在5.3节中讨论),因此最好保持不变。
进一步地,我们还在训练中引入了缺失数据注入:我们将 $λ$ 比例的正常点随机设置为零,就好像它们是缺失点一样。 缺失点更多,当给定异常 $x$ 时 ,会更频繁地训练Donut来重建正常点,从而增强了M-ELBO的效果。 该注入在每轮 epoch 之前完成,并且在Epoch 结束后恢复点。 图3中的Training步骤显示了这种丢失的数据注入。
Detection
与仅为一个目的而设计的判别模型(例如,为仅计算分类概率 $p(y|x)$ 而设计的分类器)不同,像VAE这样的生成模型可以得出各种输出。 在异常检测的范围内,观察窗 $x$ 的可能性(即VAE中的 $p_{\theta}(\mathbf{x})$ )是重要的输出,因为我们想知道给定的 $x$ 遵循正常模式的程度。可以采用蒙特卡洛方法来计算 $x$ 的概率密度 。尽管在理论上有很好的解释,但实际上,对先验样本进行采样实际上并不能很好地完成工作,如第4段所示
与其对先验进行采样,不如通过变分后验 $q_{\phi}(\mathbf{z} | \mathbf{x})$ 来推导有用的输出。一种选择是计算出 $\mathbb{E}_{\boldsymbol{q}_{\phi}(\mathbf{z} | \mathbf{x})}\left[p_{\theta}(\mathbf{x} | \mathbf{z})\right]$ 。尽管与 $p_{\theta}(\mathbf{x})$ 相似,它实际上不是一个定义很好的概率密度。另一种选择是计算在[2] 中采用的 $\mathbb{E}_{\boldsymbol{q}_{\phi}(\mathbf{z} | \mathbf{x})}\left[\log p_{\theta}(\mathbf{x} | \mathbf{z})\right]$ ,称为“重建概率”。由于在异常检测中只关注异常评分的顺序而不是确切值,因此我们遵循[2]并使用后者。或者另一个可选项,如[36]所示,ELBO(等式Eqn 1)也可用于近似 $\log p_{\theta}(\mathbf{x})$。然而,在ELBO的另外一项 $\mathbb{E}_{q_{\phi}(\mathbf{z} | \mathbf{x})}\left[\log p_{\theta}(\mathbf{z})-\log q_{\phi}(\mathbf{z} | \mathbf{x})\right]$ 使其内部机制难以理解。 由于[36]中的实验不支持该可选方法的优越性,因此我们选择不使用它。
在检测期间,测试窗口$x$中的异常点和缺失点可能给映射的 $z$ 带来偏差,并进一步使重建概率不准确,这将在5.2节中讨论。 由于缺失点始终是已知的(称为“null”),我们有机会消除缺失点所带来的偏差。 我们选择采用经过训练的VAE的基于MCMC的缺失数据插入imputation技术,该技术由[32]提出。 同时,我们在检测之前不知道异常点的确切位置,因此无法对异常采用MCMC。
更具体地,测试 $x$ 被划分为观察部分和缺失部分,即 $\left(\mathbf{x}_{o}, \mathbf{x}_{m}\right)$。一个 $z$ 样例从 $q_{\phi}\left(\mathbf{z} | \mathbf{x}_{o}, \mathbf{x}_{m}\right)$ 中获取,然后一个重建样例 $\left(\mathbf{x}_{\boldsymbol{o}}^{\prime}, \mathbf{x}_{m}^{\prime}\right)$ 从 $p_{\theta}\left(\mathbf{x}_{\boldsymbol{o}}, \mathbf{x}_{m} | \mathbf{z}\right)$ 中获取得到。$\left(\mathbf{x}_{o}, \mathbf{x}_{m}\right)$ then由 $\left(\mathbf{x}_{\boldsymbol{o}}, \mathbf{x}_{m}^{\prime}\right)$ 替换,即观察点是固定的,缺失点被设置为新值。 这个过程迭代 M次,然后最终的 $\left(\mathbf{x}_{o}, \mathbf{x}_{m}^{\prime}\right)$ 被用来计算重建概率。在整个过程中,中间值$\mathbf{x}_{m}^{\prime}$会越来越接近正常值。给定足够大的M,可以减少偏差,并且可以获得更准确的重构概率。 MCMC方法在图5中说明,并在图3的“检测”步骤中显示。
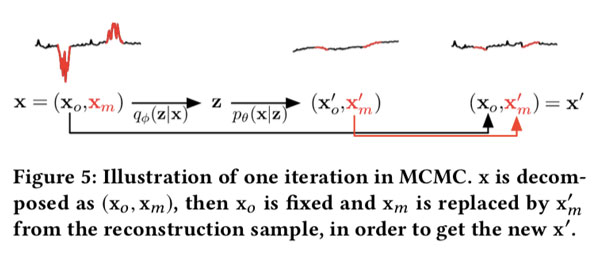
MCMC之后,我们取z的L个样本通过蒙特卡洛积分来计算重构概率。 值得一提的是,尽管我们可以计算x的每个窗口中每个点的重建概率,但我们仅使用最后一个点的分数(即$x_t$ 在 $x_{t-T+1}, \ldots, x_{t}$),因为我们想要将在检测过程中尽快归纳异常 。后续文章中我们仍将使用矢量符号,它们与VAE的体系结构相对应。 尽管可以通过延迟决策并在不同时间考虑同一点的更多分数来提高检测性能,但我们将其留作将来的工作。
Reference
1,Xu H, Chen W, Zhao N, et al. Unsupervised anomaly detection via variational auto-encoder for seasonal kpis in web applications[C]//Proceedings of the 2018 World Wide Web Conference. 2018: 187-196.

