Evaluation实验
Datasets
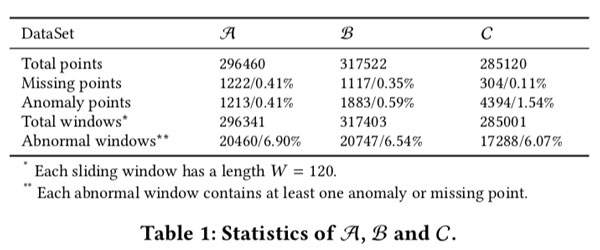
我们从大型互联网上获得了18个维护良好的商业KPIs(时间跨度足以进行培训和评估),所有的KPIs间隔为1min。三个数据集 A B C 如图6的Table1。因此我们可以评估Donut在不同级别的噪声。 我们将每个数据集分为训练集 49%,验证集21%和测试集30%。
Performance Metric度量指标
评估中,完全忽略了所有算法在缺失点(“空”)的输出。本文所有评估的算法为每个点计算一个异常分数,选择一个阈值来进行决策:如果某个点的分数大于阈值,则应该触发警报。这样,异常检测就类似于分类问题,并且我们可以计算与每个阈值相对应的精度和召回率。给定所有可能的阈值,我们可以进一步计算AUC,即召回率的平均精度。或F分数,它是给定一个特定阈值的精度和召回率的谐平均值。我们还可能枚举所有阈值,获得所有F分数,并使用最佳F分数作为度量。给定最佳全局阈值,最好的F分数表示模型在特定测试集上的最佳性能。在实践中,最佳F分数与AUC基本一致,除了细微差异(见图8)。相比AUC我们更喜欢best F-score,因为在某个阈值上拥有出色的F分数比在大多数阈值上拥有高但不是那么出色的F分数更为重要。
简单评估策略:在实际应用中,操作员通常并不关心逐点度量。 如果延迟不太长,触发连续异常段中任何点的警报都是可接受的。 已经提出了一些用于异常检测的度量来适应这种偏好,例如,[22 NAB],但是大多数度量没有被广泛接受,这可能是因为它们太复杂了。 相反,我们使用一种简单的策略:如果可以通过选定的阈值检测到真实异常段中的任何点,那么我们就说该段被正确检测了,并且将该段中的所有点都视为可以被此段检测到。 同时,异常段外的点将照常处理。 然后相应地计算精度,召回率,AUC,F-score和best F-score。 图7中说明了这种方法。alert delay = 警报分段中第一个点与第一个检测到的点之间的时间差。

Experiment 启动
参数设置:我们设置窗口大小W = 120,即2h。W的选择受到两个因素的限制。 一方面,W太小将导致模型无法捕获模式,因为模型被期望识别出那些仅来自窗口的正常模式,(请参阅第5.1节)。 另一方面,W太大会增加过度拟合的风险,因为我们用没有权值共享的全连接层,因此模型参数的数量与W成正比。我们将B和C的潜在维度K设置为3,因为3维空间可以很容易地可视化以便分析。隐藏层的 $q_{\phi}(\mathbf{z} | \mathbf{x})$ 和 $p_{\theta}(\mathbf{x} | \mathbf{z})$ 都选择作两个ReLU层,每个ReLU层具有100个单位,这使得变分和生成网络具有相等的大小。我们没有对隐藏网络的结构进行详尽的搜索。
其他超参: std 层的 $\epsilon = 10^{-4}$ ,injection ratio = $\lambda$ , MCMC 迭代次数M = 10, 蒙特卡洛积分的采样数量$L = 1024$ ,训练的batch size = 256,运行250 Epochs,优化器是 Adam[15],初始学习率是 $10^{-3}$ ,每过10Epochs就将学习率折0.75,对隐藏层采用L2正则化其系数coefficient = $10^{-3}$。 我们按标准裁剪clip梯度,限制为10.0。
标签说明:为了评估没有标签的Donut,我们将忽略所有标签。 对于偶有的标签,我们对训练和验证集的异常标签进行下采样,以使其包含10%的标记异常。 请注意,缺失点不会被下采样。 我们一直随机丢弃异常片段,其概率与每个片段的长度成正比,直到达到所需的下采样率。 我们使用这种方法,而不是随机丢弃单个异常点,因为KPI是时间序列,并且每个异常点都可能泄漏有关其邻近点的信息,从而导致性能被高估。 这样的下采样完成了10次,这使我们能够进行10个独立的重复实验。 对于每个数据集,总体而言,我们有三个版本:0%标签,10%标签和100%标签。
总体性能
我们比较AUC,best F-score和平均alert delay,与三种算法相比,如图8:
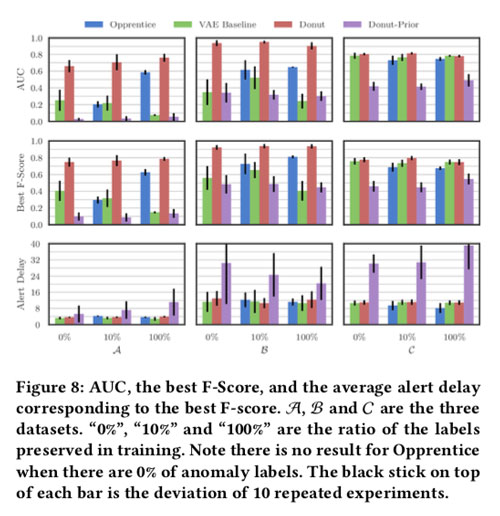
比较的算法:Opprentice[25],VAE baselin[2] 基于VAE的异常检测不处理时间序列,因此我们按以下方法设置VAE基模型。 首先,VAE基模型具有与Donut相同的网络结构,如图4所示。其次,在图3中的所有技术中,仅使用“数据准备”步骤中的那些技术。 第三,正如[2]所建议的,我们从训练数据中排除所有包含标记异常或缺失点的窗口。 Donut-Prior算法,给定一个生成模型自然学习 $p(x)$ ,而在VAE $p(x)$ 被定义为 $\mathbb{E}_{\boldsymbol{p}_{\theta}(\mathbf{z})}\left[p_{\theta}(\mathbf{x} | \mathbf{z})\right]$ ,我们还评估了重建概率的先前部分 $\mathbb{E}_{p_{\theta}(\mathbf{z})}\left[\log p_{\theta}(\mathbf{x} | \mathbf{z})\right]$。 我们只需要先验的基模型,因此我们可以通过简单的蒙特卡洛积分来计算先验期望,而无需使用先进的技术来改善结果。
The best F-score of Donut is quite satisfactory in totally unsu- pervised case, ranges from 0.75 to 0.9,
Donut,Opprentice和VAE Baseline的平均警报延迟在所有数据集中都是可接受的
Donut技术的效果
我们提出的三种技术的各自的作用(1) M-ELBO (Eqn (3)), (2) missing data injection, and (3) MCMC imputation。我们通过这些技术的四种可能的组合展示了Donut的最佳F分数:
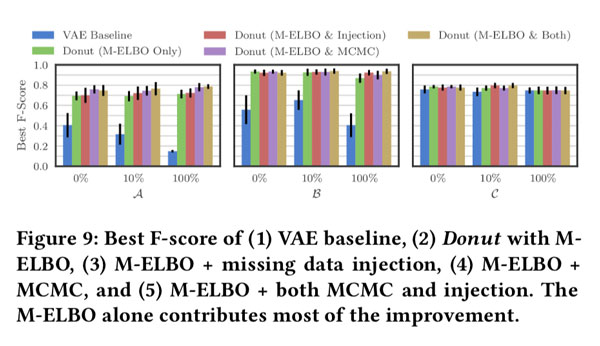
仅M-ELBO就能在VAE基模型上做出大部分改进。 它通过训练Donut来适应x中可能出现的异常点并在这种情况下产生所需的输出而起作用。尽管对于生成模型来说很自然(第5.2节),但仅使用正常数据来训练VAE以进行异常检测不是一个好习惯。
丢失数据注入是为增强M-ELBO的效果而设计的,实际上可以看作是一种数据增强方法。我们仅注入遗漏的点。由于缺少数据注入而导致的最佳F分数的提高不是很明显。注射会给训练带来额外的随机性,因此需要更大的训练时间。
MCMC imputation还旨在帮助Donut处理异常点。 尽管Donut仅在某些情况下使用MCMC获得了最佳F评分的显着改善,但它从未损害性能。 根据[32],这应该是预期的结果。 因此,我们建议在检测中始终采用MCMC。
分析K的影响。
$z$ 的维度 K很重要。K太小可能会导致拟合不足或次优平衡(请参见第5.4节)。 另一方面,K太大可能会导致重建概率无法找到好的后验概率(请参阅第5.1节)。 在完全不受监督的情况下很难选择一个好的K,因此我们将其留作未来的工作。
Analysis
我们在此提出针对重建概率以及整个Donut算法的KDE(内核密度估计)解释。

