CauseInfer的系统概述与工作流
概述
两层因果关系图:将诊断问题公式化为根因推断问题。为了推断服务和系统指标之间的根本原因,我们将运行中的分布式系统映射到两层分层的因果关系图 two layered hierarchical causality graph。 因果关系图中的每个有向边代表直接的“因果关系”关系。“因果关系cause effect”的合理基础是 原因指标cause metric的变化会导致影响指标effect metric的变化。
较高的层是由服务依赖关系组成的粗粒度因果关系图,用于将故障原因定位到正确的服务。与NetMedic [15]不同,我们通过分析两个服务之间的通信延迟相关性(traffic lag correlation)来构造服务依赖关系图。
较低的层是由系统指标组成的细粒度因果关系图,用于定位到正确的指标。指标因果关系图是通过“因果关系cause effect”概念而不是传统的“相关correlation”概念构建的。
CauseInfer的工作流workflow
CauseInfer的核心模块是因果图生成器和推理引擎。
因果关系图构建器可以使用收集的系统指标自动构建因果关系图。
推论引擎负责推导因果关系图中的真正罪魁祸首。
在目标云系统中,每个节点都维护一个指标因果图。
推断inference是由前端中的SLO违规触发的,然后沿着服务依赖关系图中的路径从前端服务迭代传递到后端服务。
如果在一个节点中检测到SLO违规,则根据指标因果关系图进行细粒度的推断。 在本文中,我们将使用第4.1节中描述的统一指标标准TCP请求延迟来表示特定服务的SLO度量标准。
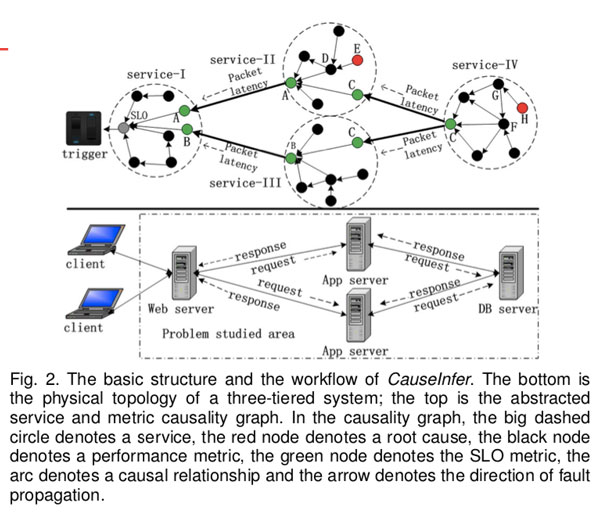
CauseInfer的基本结构和工作流程。 最底层是三层系统的物理拓扑。 顶部是抽象的服务和指标因果关系图。 在因果关系图中,大虚线圆圈表示服务,红色节点表示根本原因,黑色节点表示性能指标,绿色节点表示SLO指标,弧线表示因果关系,箭头表示方向 故障传播。
举例:我们假设服务II节点中的指标E是根本原因。 当检测到服务I的SLO违反时,将触发原因推断。 在对服务I节点进行原因推断后,我们将性能异常定位于指标A。指标A是服务II的响应时间,它也是服务I指标因果关系图中的根本原因节点。异常A意味着 服务II的SLO被违反。
因此,服务II节点中的根因推断被触发,并根据该节点的指标因果关系图继续进行推断。 最后,我们获得了根本原因,度量E。整个推理路径为SLO→A→D→E。
值得注意的是,由于统计误差和系统噪声,结果可能包含多个度量。 因此,必须有根因排名过程来减少误报并选择最可能的根本原因。
系统设计——系统模块简介
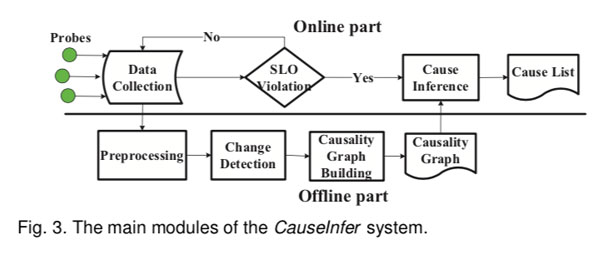
如图3所示,CauseInfer系统主要包含两部分,即离线因果图构建和在线原因推断。
在线部分包含两个模块,即数据收集模块和原因推断模块。 数据收集模块从特定节点中的多个数据源收集实时系统指标,并将数据存储在时间序列数据库中。 当检测到违反SLO时,将触发根因推断模块。 该模块负责根据因果图生成器生成的因果图来精确定位和排序根因。 最后,获得包含最可能原因的原因列表。
离线部分包含三个模块,即预处理模块,突变点检测模块和因果图构建模块。 预处理模块在发送到下一阶段之前会对数据进行一些修改。 突变点change point detection检测模块使用贝叶斯change point检测方法将每个预处理指标转换为二进制数据序列。 因果关系图模块利用二值化数据来构建两层分层的因果关系图。 在下文中,我们将详细描述这些模块。
系统设计——详述
数据收集
时序数据收集:我们的目标是确定由根本原因(例如配置错误,过载,资源占用,软件错误等)引起的性能问题的根源。因此,数据收集模块应收集足够多的运行时信息,从应用程序、流程processes到操作系统的不同软件堆栈的多个数据源。当前CauseInfer仅支持数字数据,但不包括非数字数据,例如日志事件,非数字配置项等。
SLO标准指标TCP时延:对于基于云或以云为中心的服务,最终用户体验是关键。一个特定应用程序的SLO指标(例如响应时间)可以直接显示最终用户的体验。SLO指标针对不同的应用程序而有所不同。因此,我们提出了一个新的统一SLO度量标准,即TCP请求等待时间(TCP LATENCY)。通过测量通过特定网络端口的最后一个入站数据包(即请求)和第一个出站数据包(即响应)之间的等待时间来获得TCP延迟。尽管此指标很简单,但在我们的系统中效果很好。
其他指标获取:对于与流程processes和操作系统相关的指标,我们使用操作系统随附的工具(例如,Linux OS中的/ proc文件系统)收集它们。 除了两个指标标准(即每个进程发送的数据包数量以及内核空间和用户空间的锁lock状态)外,大多数系统度量标准都可以通过这种方式获得。 为了获得前一个指标,我们通过探测与网络传输相关的kprobes [20](例如netdev.transmit)来捕获信息。 同样,我们通过探测相应的Kprobes来捕获锁定状态。 这些Kprobes已合并到主流Linux操作系统中。
数据预处理
Data aggregation:看到一个应用程序生成多个具有相同名称的进程processes来提供服务的情况并不少见。 例如,Apache httpd在Linux操作系统中总是生成多个具有相同名称“ httpd”的进程来处理Web请求。 在这种情况下,我们将这些流程的绩效指标聚合在一起。
Metric selection:图4,一些指标高度相关correlation,需要减少冗余指标。
指标选择以简单的成对方式进行:如果两个指标的Pearson相关系数的绝对值超过预设阈值(在本文中为0.8),则将其中一个消除。 例如,在图5中,CPU Int和CPU Irq的相关系数接近1。因此,我们将从CPU Int和CPU Irq中随机选择一个。
但是对于那些预定义的根因指标(例如工作量workload和配置项configuration),我们将始终将其保留在指标集中。
构建算法
离线change point detection
cause-effect定义:如果一个变量变化导致另一个变量变化,则这俩者有因果关系。
首先识别系统指标里的changes突变。这可以被认为是离线分割问题。 但是挑战在于细分的数量,每个细分中的统计特征(即均值或方差)事先未知。 我们介绍了一种基于贝叶斯理论的新颖方法,即贝叶斯变化点检测(BCP)[22]。 变更点检测过程不仅提取变更,而且以二进制格式统一不同尺度的不同系统的指标,这意味着度量数据仅包含“ 0”(未更改)和“ 1”(更改)。
BCP的基本思想**(paper的P5):是找到一个参数的基本序列,该序列将时间序列划分为具有相等参数值的连续块(序列块),并定位突变点的位置,即每个块的开始。
给定块和参数,不同块中的观测值是相互独立的。 应该给每个块的突变点和参数一个先验的概率分布 $\mu_{i,j}$ (是在位置i+1开始在j结束的块的均值)服从 $N\left(\mu_{0}, \sigma_{2}^{0} /(j-i)\right)$
给定观测序列:$X=\left(x_{1}, x_{2}, \cdots, x_{n}\right)$ ,目标是找到划分 $\rho=\left(P_{1}, P_{2}, P_{3}, \cdots, P_{n-1}\right)$ ,如果$P_i = 1$ ,则表示位置i+1有一个变化change。$\theta_i$ 表示$x_i$所在的划分P的统计参数。
Barry报告,参数序列$\theta_i$ 形成一个马尔可夫链:以概率$ 1 -p_i$ 假设 $\theta_i = \theta_{i+1}$ ,即$x_i,x_{i+1}$ 是属于相同的划分 ,or或者说以概率 $p_i$ 存在一个条件密度 $f\left(\theta_{i+1} | \theta_{i}\right)$ 。因此,我们使用一个马尔可夫蒙特卡洛法来计算一个近似划分。
在马尔可夫链的每一层转移,根据观测值的序列和 $P_j$ 的当前值,从$P_i$的条件分布中获得 $P_i$ 的值 ,$j \neq i$。在迭代的开始,我们为所有i都初始化 $P_i = 0$ 。转移概率 $p_i$ ,对于位置 $i+1$ 处的突变点的条件概率可以通过以下公式估计(参考论文22,这些表达式的参数设置):
因此我们可以获得 $f\left(P_{i}=1 | X, P_{j}, j \neq i\right)$ 和 随机采样$P_i$ 。在一次MCMC迭代中,为每个$P_{i}(1 \leq i \leq n)$ 产生一个值。每次迭代,后验均值$\mu_{i, j}$ 将根据当前划分进行更新。M次迭代以后,我们利用 $\mu_{i, j}$ 的M个估计的平均值作为给定X的后验均值的近似值。类似地,在给定$X$的情况下,我们可以获得$\sigma^2$的后验估计。同时,获得了概率$p_i$。 本文,M设置为1000足以估计参数。 最后,选择具有高概率 $p_i$ 的突变点(例如,本文中pi> 0.6)作为变化。
为了评估BCP的有效性,我们利用它来确定从第4节中描述的CPU故障注入实验获得的CPU TOTAL指标的更改点。我们通过手动调查确认在CPU TOTAL度量标准中嵌入了16个更改点。 图5(a)显示了在注入多个CPU hog故障以及BCP检测到更改点时的CPU利用率数据。 从该图可以看出,几乎所有的变化都发生在CPU hot fault期间。 图5(b)表明,在CPU出现hog故障期间发生变化的可能性非常高,远大于0.6。 因此,BCP方法可以有效地识别嵌入在数据序列中的更改。 但是,由于BCP需要较长的历史数据和计算复杂性,因此利用BCP实时检测实时变化并不容易。
随机图的构建 Causality graph building
$X \rightarrow Y$ X直接影响Y,表示为$X \in p a(Y)$ ,不允许两个变量相互影响。 因此,所有因果关系都可以通过有向无环图(DAG)进行编码。在DAG中,节点代表特定变量,边代表因果关系。 我们依靠观察和假设来形成因果关系理论。
Service Dependency Graph
流量关联方法是一种通用的轻量级方法,无需更改源代码或准备其他知识。基本思想是两个相关服务之间的流量延迟通常表现出“典型”峰值,反映了使用或提供这些服务之间的潜在延迟。 a,我们的方法仅关注使用TCP作为其底层传输协议的有限应用程序集,尽管可以很容易地对其进行扩展。 b, 我们的方法依赖于现代操作系统的新属性,例如网络统计工具和用于探测系统调用的内核探测器。 C,我们利用流量延迟来确定依赖方向,而不是确定依赖结构。
我们使用两元组(ip,服务名称)而不是三元组(ip,端口,协议)来标识服务。在分布式系统中,ip表示唯一的主机,服务名称表示在主机中运行的唯一服务。 我们遵循Orion系统中服务依赖项的定义,即如果服务A需要服务B来满足其客户端A→B的某些请求。例如,Web服务需要从数据库服务维护的数据库中获取内容,因此 我们说Web服务取决于数据库服务。
该方法开始于使用连接信息来构造服务依赖图的框架。 借助一些现成的网络监控工具(例如netstat),我们获得了所有服务连接信息的列表,包括协议,源IP,目标IP,端口和连接状态(例如,侦听或已建立)。 然后,我们从一堆由TCP协议标记的实时连接中筛选出源和目标信息。 图6展示了一个节点中选定的连接对样本。 每个连接的格式为 source ip : port → destination ip : port, which is called a channel称为通道。 该通道非常接近服务依赖关系,但缺服务的名称。
进程ID(即PID)。然后,我们将与PID有关的命令行用作服务名称。
通过网络发现两个通信服务之间的服务依赖关系:为了获得特定服务的发送流量,我们通过探测内核函数netdev.transmit来计数数据包的数量,该函数在网络设备要发送缓冲区内容时调用。 假设X表示服务A的发送流量,Y表示服务B的发送流量,则X和Y之间的滞后相关性lag correlation定义为:
if $k^{*}>0 , A \rightarrow B$
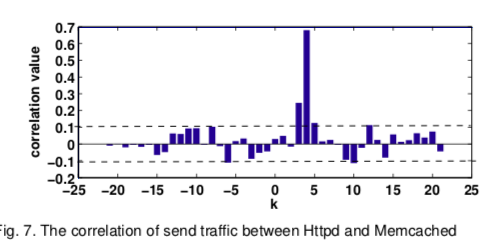
由于资源共享,服务可能依赖于在同一节点中运行的其他服务,这被称为“非通信服务依赖性”。 考虑到这种间接依赖性,我们假设其他服务的性能指标的变化也影响当前关注的服务的性能指标的变化。 我们在指标因果关系图中建模这些依赖关系,在以下部分中进行了说明。
Metric Causality Graph
我们利用条件独立性检验[ 参考 26]而非成对相关 pair-wise correlation 来构建因果关系图。 基于“因果关系cause effect”概念构建因果关系图的方法主要有两种,即条件独立性测试和基于评分score based的方法。 考虑到系统指标的高维性和轻量级需求,我们基于PC算法(unsupervised leaning)设计算法。
DAG 有向无环图。两假设:causal Markov condition and faithfulness (31)
作为区分因果关系和相关性的基本属性,因果马尔可夫条件用于在两个以上变量之间产生一组独立关系,并构造因果图的框架。
忠实性假设指出存在一个有向无环图,G,使得V中变量之间的独立关系正是通过条件马尔可夫条件并由G表示的[26]。 因果关系可以通过因果马尔可夫条件与忠诚条件相结合来发现。
在这两个假设下,PC算法根据统计条件独立性检验[26] [31]和D-separation [26] [31]为集体变量构造一个DAG。 在本文中,我们利用基于条件交叉熵的度量$G^2$ [31]定性地测试给定 $Z$ 时 $X$ 是否依赖于 $Y$,其中X,Y和Z是V中不相交的变量集,X和Y是单变量,但是 Z可以是一组变量。
m: sample size
$C E(X, Y | \mathbf{Z})$ the conditional cross entropy of X and Y given Z.
度量$G^2$服从$\chi^{2}$ ,自由度是:$\left(N_{X}-1\right)\left(N_{Y}-1\right) \prod_{Z^{\prime} \in \mathbf{Z}} N_{Z^{\prime}}$
$N_{X}, N_{Y} ,N_{Z^{\prime}}$ 各自代表变量 $X ,Y, Z’$ 的值。卡方测试我们可以决定是否接受独立性假设。$p > \xi$ 接受独立性假设。
给定 $Z$ 如果 $X$ 独立于 $Y$ ,则 $I(X, Y | \mathbf{Z})=1$
PC算法从完全连接的无向图开始,然后促进 $G^2$ 以成对方式捕获所有变量中的所有独立关系,即该DAG的骨架。 以下工作是使用D-separation[26],[32]确定因果关系的方向。
确定因果关系的方向:
我们首先为aggressive(没有先验知识)算法准备系统指标。对于没有任何依赖服务的服务(例如数据库服务),因果关系图仅使用本地系统指标来构建。
但是对于具有依赖服务(例如Web服务)的因果关系图,不仅使用本地系统度量标准,而且还使用其依赖服务的TCP LATENCY度量标准来构建。
为了诊断由共置co-located服务引起的性能问题,我们将其系统指标集成到此算法中。本文中训练数据的长度设置为200,因为200个数据点足以建立精确的因果图。
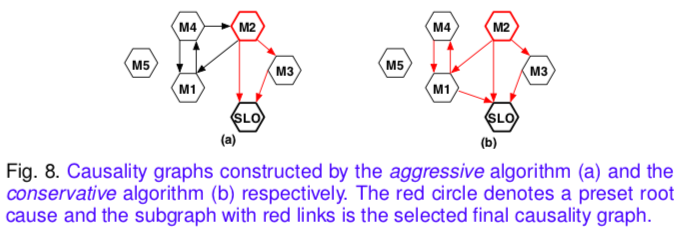
然后,我们采用PC algorithm构建DAG。由于缺乏证据,统计错误或非因果关系,获得的DAG可能包含多个孤立的子图,违反直觉的因果关系和双向链接。例如,在图8(a)中,M5是隔离的,因果关系M 4→M 2是反直觉的,并且M 1和M 4之间的因果关系是双向的。
为了从SLO指标推断出根本原因,我们进一步使用以下规则从DAG中选择一个最大子图。规则1:作为最终effect metric的本地服务的TCP LATENCY指标没有后代。
规则2:最终指标可从图中的任何路径可达。
规则3:对于双向链接,两个方向均被保留,这意味着两个指标标准可能在彼此之间引起影响。
aggressive algorithm in Algorithm 1 伪代码(见paper):
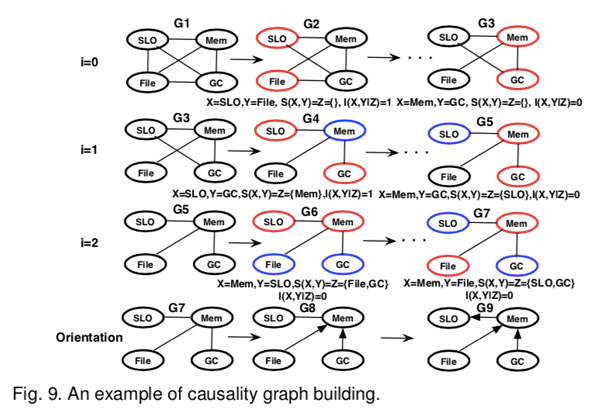
step1,设置i=0,即$z=\{\}$ ,选择两个指标用 $G^2$ 方法测试他们的独立性。如SLO独立于在G2(Fig9)中的文件,即$I(S L O, F i l e)=1$ ,则将它们俩之间的边移出。
step2:然后当i = 1和i=2时,测试独立性。在G6中,给定Mem,SLO条件独立与GC,即$I(S L O, G C | M e m)=1$ ,因此 $M e m \in S(S L O, G C)$
step3:当i=3,停止条件$\left|a d j\left(G^{u}, X\right)\right| \leq i, \forall X$ 满足。最终得到架构图如G7。
step4:接下来,根据算法中提到的规则确定方向。首先,G8 as $\operatorname{Mem} \notin S(F i l e, G C)$ ,然后“Mem —— SLO” 被 “ Mem ——> SLO”替代。
最终的causality graph如G9。使用因果图G9,可以查明Hadoop-3382错误的根本原因。 CauseInfer首先使用服务依赖关系图将异常定位在名称节点上,然后在G9中沿路径“ SLO→Mem→File”找到根本原因“ File”。
在本文中,我们将ξ设置为0.2以在开销和准确性之间进行权衡。
保守算法:首先要初始化完全无向图Gu中的某些方向。 TCP LATENCY和其他度量标准之间的链接是直接的。 指向预设根本原因指标和其他指标之间的链接。 第二点是在子图选择过程中添加另一个规则,即规则4,因为先验知识得到了补充。
在线根因推断
当在前端检测到SLO违规时,将触发原因推断。 我们首先使用指标因果关系图推断本地服务的根本原因。 如果根本原因位于本地服务的从属服务的SLO度量标准上,则将推理过程传播到远程从属服务。 该过程将反复进行,直到未发现任何违反SLO的情况或未找到相关服务为止。 请注意,图中的推断方向与因果方向相反。
为了实时检测SLO指标和其他系统指标的异常,我们采用流行的CUSUM [8]。$X(t)=\left\{x_{1}, x_{2}, \cdots, x_{t}\right\}$ 代表X的观测序列,如果在包括新的到达数据后统计属性发生变化,则会发生异常。$x_k$ 是否是突变基于对数似然比检验。
CUSUM statistic score is updated :
$P_i(x_k)$ 代表假设$H_i$下$x_k$的概率,相应的决策规则是:given a threshold h, 1 represt change
为了推断特定节点中的根本原因,我们使用深度优先搜索(DFS)方法遍历度量因果关系图。当遍历图中的度量时,我们使用CUSUM来检查它是否异常。如果异常,我们将继续遍历其后代。否则,我们遍历其兄弟姐妹。如果没有任何异常指标的后代或所有后代中都没有违规,则将该指标视为根本原因。
图8(b)为例,当S LO异常时,我们从度量S LO开始推理过程。然后,我们调查指标M1。如果正常,则遍历其同级之一,即M2。如果M2异常,则是根本原因。 M2的另一个兄弟是M3。如果M3异常,我们将继续检查M2。由于M2异常,因此将M2作为根本原因。最终,尽管M 2和M 3均异常,但我们仅找到一个根本原因M 2。但是,在基于“相关”的方法中可能并非如此。由于存在多种因果路径,因此在某些情况下有可能获得一组潜在的根本原因。因此,有必要对最可能的原因进行排名和选择。在本文中,我们根据其CUSUM得分对根本原因进行排名。 CUSUM得分最高的根本原因将放在原因列表的顶部。
Reference
1, Chen P, Qi Y, Hou D. CauseInfer: automated end-to-end performance diagnosis with hierarchical causality graph in cloud environment[J]. IEEE transactions on services computing, 2016, 12(2): 214-230.

