组合优化问题
问题引入
车辆路径规划问题,n位客户,在不同地点,有需求。在中央仓库有m辆车辆的均质车队。这是一个NP难问题,这类问题中,启发式和元启发式是实践中最常用的VRP解决方案。
启发式算法:模拟退火,遗传算法,蚁群优化算法等。
NP难问题的一些解决方法
1,精确方法(枚举,约束编程,分支定界,分支与剪切)是非多项式的,通常可以处理一定规模的问题实例(如旅行商问题TSP的80000节点)。
大量的问题实例可以有效地解决(例如,区间图的顶点着色问题)
2,一些指数算法仅取决于问题实例的一个参数=>参数化算法(包括伪多项式算法)
3,近似算法
4,随机算法
5,启发式方法和元启发式方法可以视为最后的选择。但他们生成的解决方案没有任何性能保证。
局部搜索启发式
局部搜索
local search局部搜索启发式迭代地优化解。 它枚举了导致新解(称为邻居neighbor)的可能更改(move)的列表,并在改进的情况下应用这些更改(接受更好的解)。
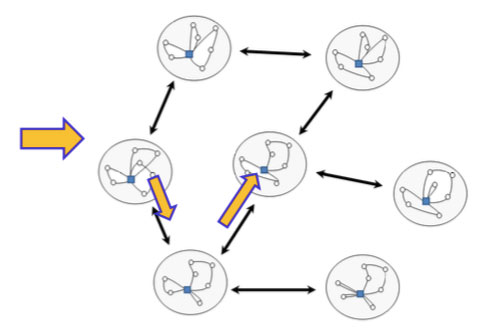
仅应用这些邻域会导致问题的局部最优,这可能与最佳解决方案(全局最优)大不相同。需要设计了几种策略来摆脱这些局部最优值,并继续在其他地区进行搜索。
解决局部最优
1,允许坏解的运动 deteriorating moves(模拟退火)
2,在解决方案上施加扰动perturbation以将其移至其他位置
3,更改邻居(可变邻居搜索variable neighborhood search)
4,惩罚当前的局部最优值
5,同时保留多个解(填充),然后将它们交叉在一起以生成新的起点(带有交叉算子的遗传算法)
6,重复一个建设性的过程来创建新解,并根据先前解中的成功(信息素)来促进良好的建设决策(如蚁群优化/强化学习)。
metaheuristic定义
元启发法被正式定义为一种迭代生成过程,该过程通过组合智能的不同概念来探索和利用搜索空间来引导从属启发法,并使用学习策略来构造信息,以便有效地找到接近最优的解决方案
一些特点:目标是有效地探索搜索空间以找到高质量的解,允许逃出局部最优,方法的抽象级别描述,元启发法通常是不确定的,最近的元启发法会从他们过去的搜索经验中“学习”以指导搜索。
理论分析
三种启发式
Constructive heuristic
1,Constructive heuristic 构造性启发式:将解决方案构造为一系列决策选择,而后无需修改这些选择,一般针对问题量身设计。如今,经常用作更复杂的解决方案方法的子组件,以生成初始解决方案或作为解决方案过程的一部分。
2,适用场景:
local search 难的问题。比如,针对不等面积设施布局问题的有偏随机密钥遗传算法,EJOR,2015年。
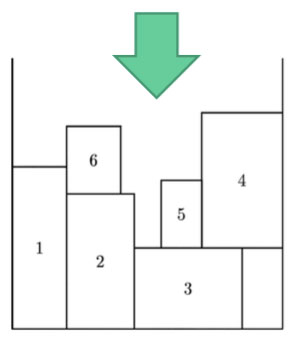
用作解决方案解码器 decoder。如,An Exact Approach to the Strip-Packing Problem, INFORMS J. Comput., vol. 15, no. March 2015, pp. 310–319, 2003.
metaheuristic元启发式的组成部分(GRASP,蚁群优化,破坏再重建方法)。
3,方法
贪心算法:每次赋值给一个决策变量,逐步构建出一个解。每一步都选择成本最低的决策。三种贪心策略(TSP1,TSP2,)
TSP1 : nearest-neighbor heuristic 最近邻居启发式算法。时间复杂度 $O(n^2)$
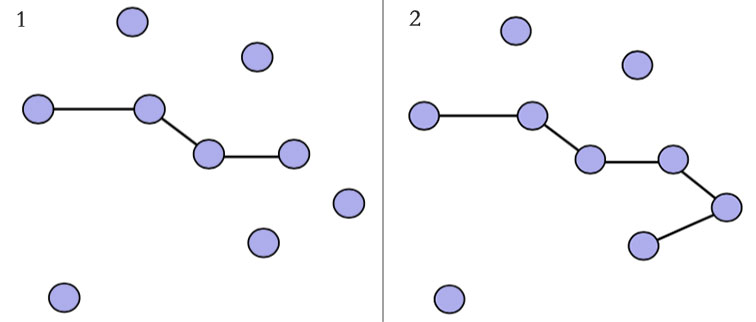
如图,我们选择离当前点最近的路径。
TSP2:cheapest-insertion heuristic 最小代价插入
Reference
1,书籍文章参考
M. Gendreau and J.-Y. Potvin, Eds., Handbook of Metaheuristics, third edition, 2019.
E.K. Burke and G. Kendall, Eds., Search Methodologies — Introductory Tutorials in Optimization and Decision Support Techniques. Springer, 2014.
E.G. Talbi, Metaheuristics: from design to implementation, Wiley Series on Parallel and Distributed Computing, 2009
C. Blum and A. Roli, “Metaheuristics in Combinatorial Optimization : Overview and Conceptual Comparison,” ACM Comput. Surv., 35(3), 268–308, 2003.
2,罗志兴,课程

