从优化角度看L1正则化的稀疏性

背景

大数据背景的几个特点：量大large scale，实时性动态产生数据，结构化/半结构化数据，可信赖程度低（Noise，考虑模型如何更robust），高维度且稀疏的数据集。

这里主要说高维稀疏数据带来的一些问题：

$x=\left(x_{1}, x_{2}, \cdots, x_{p}\right)$, 特征是p维，数据样例有n个，即整个dataset是 n × p ，传统的统计方法适用于一些 n > p 的情况，但是当 n << p的时候，数据量小，但想要求的参数又很多的时候就有困难了。

Linear Regression

从最基本的模型开始来看如何解决这个问题。

X 代表输入，Y代表输出，$\varepsilon$ 是误差项。

$$Y=f(X)+\varepsilon$$

监督学习，给出数据集 $\left(X_{1}, Y_{1}\right),\left(X_{2}, Y_{2}\right), \ldots,\left(X_{n}, Y_{n}\right)$，如何估计出 $f(X)$ 呢？

也可以用一些非参数的方法：如用KNN….

还可以考虑参数方法：施加一些参数进去，我们去估计参数 $\beta_i$

$$Y=\beta_{1} X^{1}+\beta_{2} X^{2}+\cdots+\beta_{k} X^{p}+\varepsilon=\beta^{T} X$$

(这里我们比如我们画图看后，根据领域知识等，假设 f(X) 是线性的等，就用LR模型来看。)

常用方法用最小二乘法（即最小化平方损失函数）：

$$\min \sum_{i=1}^{n}\left(Y_{i}-\beta^{T} X_{i}\right)^{2}=\|Y-X \boldsymbol \beta\|^{2}$$

• 这样求解 $\beta$ 会得到很好的统计性质
• 问题存在：处理高维数据的时候 $X \in R^{n \times p}$ ，这个问题的解有多个，要取哪个？如果求解的话可以这里可以去写写 $|Y-X \boldsymbol \beta|^{2}$ 的最优性条件 KKT条件有：$X^TX \boldsymbol\beta = X^TY$ ，而这里的 $X^TX$ 是non singular，不可逆，求解有困难。
• 可解释性也不太好，这个得到的 $\beta_i$ 一般都是不为0，那Y到底跟哪个X有关呢，怎么找重要的因素去解释呢？
• 高维的时候可以考虑降维，如PCA，但也有问题，$x_1,…x_p$ 利用线性组合到一起，把某几个因素合为一个新变量，但新变量的解释也不好说。

Sparse Optimization

sparse Optimization

考虑用稀疏优化来解决。

定义稀疏结构 sparse structure：$x \in R^{p}$ 如果仅仅有少部分非0值，则称为sparse vector。

定义0范式：$||x||_0= \left\{i: x_{i} \neq 0\right\}$ 即是$x_i \neq 0$ 的个数 （如 x = (0,0,1), 则其0范数值为1）

稀疏数据问题：$||x||_0 << p$

个数限制优化 (Cardinality constrained Optimization)方法：

$$min \|Y-X \boldsymbol \beta\|^{2}$$ $$s.t. \|\boldsymbol \beta\|_{0} \leqslant k \quad(k<< p)$$

意思：最小化误差，但有约束存在 $\beta$ 的0范数小于等于 k，只有k个系数不为0，即Y只跟少数的k个X变量有关，解释性就加上了。

Integer Programming

我们把上面这个优化改写成一个整数规划来看：

$$\min \|Y-x \beta\|^{2}$$ $$s.t. \sum_{i=1}^p S_i \leq k$$ $$S_i = 0 \quad or \quad 1$$ $$\left|\beta_{i}\right| \leq M S_{i} , M - EnoughBig$$

类似一个设施选址问题的写法：两阶段，第一选不选：Si表示选不选，选了变量$X_i$，$S_i$就是1；coefficiency系数，$\beta_i$表示系数。

这样改写之后，就可以用部分求解器如CVX , Gurobi求解中等规模的问题。但是如果规模太大（ 即 p 非常大）就不好求解了。

凸近似

那我们转换整数规划为凸优化来解：

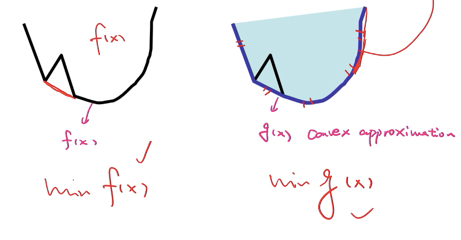
具体来看怎么转换的凸优化呢？

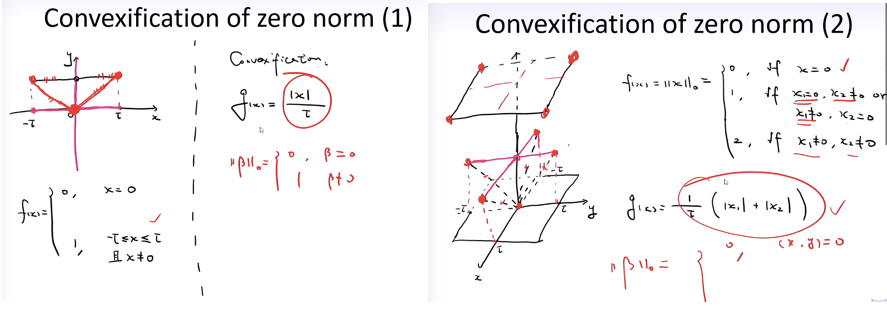
一维情况（左图）：

我们要去凸近似这个 f(x) 即zero-norm（0范数函数），当x=0时f(x)=0，当x在$-\tau \leqslant x \leqslant \tau$ （这里的$\tau$ 只是表示一个范围，可以取很大，这为了好看）时，f(x) = 1。

函数图画出来是上面那一根黑线（除开x=0中间那个空点，这个不好处理），怎么去凸近似这个函数呢？我们用函数 g(x) 去近似，即红色那个线把三个点连起来，这是最简单的，也可以考虑用二次函数椭圆形来近似也可以：

$$g(x) = \frac{|x|}{\tau}$$

二维情况（右图）：

二维的情况也可以画图来分析：就是最下面中心那个点，加上面的十字线除开中间那个点（x其中一个为1），加上最上面为2的面：

$$f(x) = ||x||_0 = \left\{\begin{array}{ll}0, & \text { If } x=0 \\ 1, & \text { If } x_{1}=0, x_{2} \neq 0 \text { or } \\ & x_{1} \neq 0, x_{2}=0 \\ 2, & \text { If } x_{1} \neq 0, x_{2} \neq 0\end{array}\right.$$

这里的凸近似，将下面的四根虚线连起来（延展上去也连上面的四个红点），就是g(x)：

$$g(x) = \frac{1}{\tau}(\left|x_{1}\right|+\left|x_{2}\right|)$$

看看上面一维、二维的情况，都与绝对值有关，是不是还有点像L1正则化的样子，我们接着看。我们总结下zero norm0范式的凸近似是：

$$\|x\|_{0}:\tau (\|x\|_{1}) = \tau \sum_{i=1}^n |x_i|$$

即存在一个 $\tau$ ，使得$\tau (|x|_{1})$ 是$|x|_{0}$最好的凸近似。

Sparse Linear Regression

typical sparse model

回忆之前的LR模型：

$$min \|Y-x \boldsymbol\beta\|^{2}$$ $$s.t.:\|\boldsymbol\beta\|_{0} \leqslant k$$

这里的约束我们就可以用前面推导的一范数来近似了：

$$\|\boldsymbol\beta\|_{1} = \sum_{i=1}^p |\beta|_{i} \rightarrow \|\boldsymbol\beta\|_{0}$$

上面的模型可以改写为：

$$min \|Y-x \beta\|^{2}$$ $$s.t. \tau\|\beta\|_{1} \leqslant k \quad (即\|\beta\|_{1} \leqslant \lambda)$$

这里的$\lambda$ 自己取。这就产生了新的模型了。

我们用图形说明看看，sparsity 是真的有的：

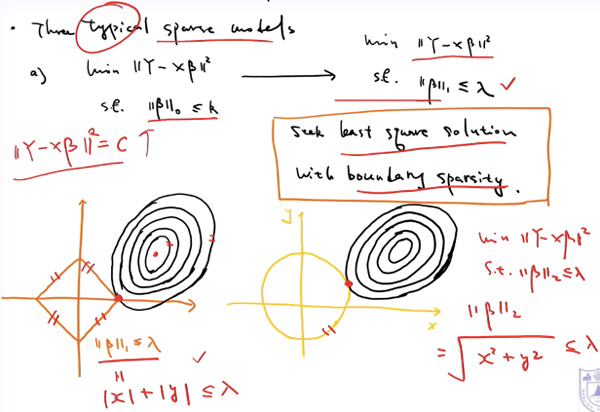
左下图：C越大椭圆越大。如果是$|\beta|_{1} \leqslant \lambda$则相交点在坐标轴上，往往是左下图红色点那里，而这个地方则很好的可见 $\beta$ 参数的非0个数 < P=2了。但如果看右边图，采用 $|\beta|_{2}$ 则相交在中间，$\beta$参数的非0个数 = P（2）了，那$\beta$ 全部都不为0，没有起到稀疏作用。

Lagrange version

我们再改写下上面的模型为拉格朗日版本，将约束放到上面相当于拉格朗日乘子：

$$min\|Y-x \beta\|^{2}+{\mu}_{1}\|\beta\|_{0} \rightarrow min \|Y-x \beta\|^{2}+{\mu}_{2}\|\beta\|_{1}$$

这里看就是既要看损失，又要看稀疏性，这两者之间有个tradeoff平衡选择。

右侧这边这个模型，在统计中也叫做lasso模型，也就是L1正则化。

总结一下，在线性回归中，我们遇到了一个高维的问题导致了参数的不稀疏，无法较好的解释。我们用稀疏优化来解决这个问题，我们把选择部分参数不为0（不为0的参数个数）这个zero norm用凸近似来做，将其转换为绝对值这个凸函数，进过改写为拉格朗日形式后，这个约束就成了L1正则化的形式。

Reference

1，南京大学，陈彩华 《高级最优化》

2，《最优化》陈宝林