高级最优化1——线性规划

高级最优化

先修条件：线性代数，最优化/运筹，基础的概率论，MATLAB使用（如何建模与使用）

优化分类

1，确定性优化：

Linear Optimization线性规划，Second order cone programming 二阶椎优化，Semidefinite programming （SDP半定优化）

以上三个优化就是现代凸优化。延伸的一些最新的优化：

Sparse and low rank Optimization（稀疏优化/低秩优化，图像视频处理用的多）

2，不确定优化：

stochastic programming（随机优化）：不确定的东西，我们假设分布函数已知，则可以用。

classical Robust Optimization（鲁棒优化）：测量一个值，一般有误差项 ，这个误差项属于某个范围之内 $\xi \sim\lceil a, b\rceil$，但不知道分布的话，可以用鲁棒优化来建模。

Distributionally robust Optimization：鲁棒优化和随机优化结合起来，知道分布的部分信息但又不完全知道。比如，$\xi \sim F \in \{Set\}$ Set是一个大的分布族，$E(\xi) = \mu , D(\xi) = \sigma^2$

本文主要涉及连续优化和不确定性优化。

五步法建模

1，认清楚问题，理解现实问题为数学问题（弄清楚问题！！！最难）

2，建立优化模型（一般是决策问题）三要素——Decision，constrain，objective function （如设施选址，决策变量是选地方，约束条件，为了什么（医院覆盖范围广，减少成本等等））

3，Feed data to model ：模型里有很多参数，从数据里得到参数。大数据时代应用多，Analytics 含statistic + ml ，用data做一些prediction ，加上优化的模型 （data to decision，数据驱动的决策，数据与运筹相结合）

4，求解模型

5，implement the solution：如果不好则返回到步骤1循环看怎么重新建模

优化模型

线性规划

线性规划常用于生产计划问题，如何安排生产，使得利润最大化。模型解法是Simplex 单纯性方法（ from Dantzig）

线性规划的标准形式：

$$min \boldsymbol{c}^{\prime} \boldsymbol{x}$$ $$\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}$$ $$x \geq 0$$

分片线性

线性规划可以扩展出很多模型的，如convex piece-wise linear objective function 凸 分片线性的：

$$\min f(x)=\max _{k}\left(d_{k}^{\prime} x+c_{k}\right)$$ $$\text { s.t. } \quad A x \geq b$$

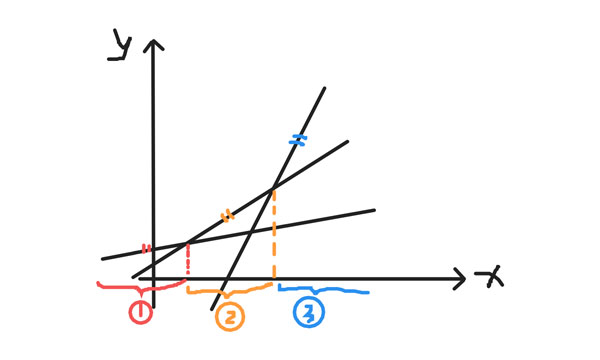
圈1，圈2，圈3分布是在x取不同值时，取最大值时的情况。再看约束，也是线性的，但目标是分段线性的了。任何一个分片线性模型就是类似这种，线性函数中取最大的形式。

我们改写上面的模型：

$$min z$$ $$s.t. Ax \geq b$$ $$\boldsymbol{d}_{k}^{\prime} \boldsymbol{x}+c_{k} \leq z$$

绝对值问题

绝对数的模型，也可以转换为线性规划求解。

$$min \sum_{j} c_{j}\left|x_{j}\right| ,(c_j \geq 0)$$ $$\text { s.t. } \quad A x \geq b$$

我们这样看，令$z_{j}=\left|x_{j}\right| = max\{x_j,-x_j\}$，就可以写为如下形式了：

$$\min \sum_{j} c_{j} z_{j}$$ $$s.t. Ax \geq b$$ $$x_j \leq z_j$$ $$-x_j \leq z_j$$

但并非所有非凸问题可以转回为凸问题，并非所有凸问题都可以转为线性规划问题。

组合拍卖—机制设计

Market for Word Cup Winner问题

information market：某个地方集中所有的信息aggregate，来做决策设计机制，稳赚不赔。

世界杯中可以赌球，假设有五个国家有可能在比赛中胜，每个人都可以生成赌球的订单order（就是赌谁赢），选择中只有赌赢了一个就可以赢 $1。引入一个market maker，他做决策接受或拒绝order，怎么做可以不亏钱。

Order	Price: pi_i	Quantity limit: q_i	Filed :x_i	Argentina：a	Brazil	Italy	Germany	France
1	0.75	10	5	1	1	1
2	0.35	5	5				1
3	0.4	10	5	1		1		1
4	0.95	10	0	1	1	1	1
5	0.75	5	5		1		1

（表里：右侧的1表示赌这个国家赢。price是售价，赌得越厉害比如order 2售价相对低一点。Filed表示market maker做的事，你订单虽然买了Quantity这么多，但maker只限制接受Filed这么多的订单。）

抽象模型

给定m状态（即只有一个国家赢，互斥的）。

order是一系列赌的决策（$a_{i1},a_{i2},…a_{im}$）（表里order 1就是（1，1，1，0，0））。

price limit是参与者愿意对某order所支付的价格 $\pi_i$。

quantity limit是参与者最多可以买多少份。$q_i$

建模Linear Programming

Filed：对order i只接受 $x_i$ ，总收入 $\sum_i \pi_i x_i$ ，对于market maker而言，如果jth个team赢了则成本是 $\sum_i a_{ij}x_i$ ，因为1美元 被赢走了嘛，整个最坏情况就是 $\max _{j=1, \ldots, m}\left\{\sum_{i} a_{i j} x_{i}\right\}$ （即某一个国家赢了导致的最大损失）

写出线性规划模型为：

$$\max \sum_{i} \pi_{i} x_{i}-\max _{j}\left\{\sum_i a_{i j} x_{i}\right\}$$ $$\text { s.t. } \quad 0 \leq x_{i} \leq q_{i} \forall i=1, \dots, n$$

第一个公式的 -max 其实等于 $+\min \left\{-\sum_{i} a_{i j} x_{i}\right\}$

也可以改写成：

$$\max \sum_{i} \pi_{i} x_{i}-w$$ $$\text { s.t. } \quad \sum_{i} a_{i j} x_{i} \leq w \quad \forall j \in S$$ $$0 \leq x_{i} \leq q_{i} \quad \forall i \in N$$

($\sum_{i} a_{i j} x_{i} \leq w $，对偶变量dual solution：影子价格，代表了资源的价格 )

建议参考书籍

–Convex Optimization,

•S. Boyd and L. Vandenberghe.

–Lecture on modern convex optimization

•A. Bental and A. Nemirovskii

–Stochastic Linear Programming

•P. Kall and J. Mayer

–Introduction to Stochastic Optimization

•J. Birge, F. Louveaux

–Robust Optimization

•A. Bental, L. El Ghaoui, A. Nemirovskii

–SHFEU Robust Optimization Course Notes

•A. Bental

Reference

1，陈彩华《高级最优化》