位数交换
第一题就是按照他的先一个数字每两位交换,然后第二步后一个数字的高两位是他前一个数字右移出来的两位,第一个数字的高两位是最后一个数字的低两位。比如输入1 2,输出是1073741824,2147483648。
1、转换成二进制01字符串,二进制字符串填充成32bit长度;
2、交换奇偶位,完成交换操作,比如0001 -> 0010;
3,对整数向右移动两位,将所有移位后的二进制字符串拼接在一起,将最后两个字符放到拼接字符的最前面,并去除这最后的两个字符,完成移位操作;
4、将最后的字符串按32bit长度划分,得到原来的n个整数的二进制字符串,将二进制字符串转换成整数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
int main()
{
vector<unsigned int> data;
char ch=' ';
while(ch!='\n')
{
unsigned int temp;
cin>>temp;
data.push_back(temp);
scanf("%c",&ch);
}
int n = data.size();
for(int i=0;i<n;i++)
{
unsigned int temp[33];
for(int j=1;j<32;j=j+2)
{
temp[j+1]= ((data[i]>>(32-j))&1)<<(32-j-1);
temp[j]= ((data[i]>>(32-j-1))&1)<<(32-j);
}
data[i]=0;
for(int j=1;j<=32;j++)
data[i]=data[i]|temp[j];
}
unsigned int t1=0,t2=0;
for(int i=0;i<n;i++)
{
int f1=t1,f2=t2;
t1=(data[i]&1)<<30;
t2=((data[i]>>1)&1)<<31;
data[i]=(data[i]>>2)|f1|f2;
}
data[0]=data[0]|t1|t2;
for(int i=0;i<n;i++)
cout<<data[i]<<" ";
return 0;
}
|
求抛物线与直线围城的面积
求抛物线 $y^2 = 2Ax $ 与直线 $y=Bx+C$ 所围城的封闭图形面积。若图形不存在,则输出0。
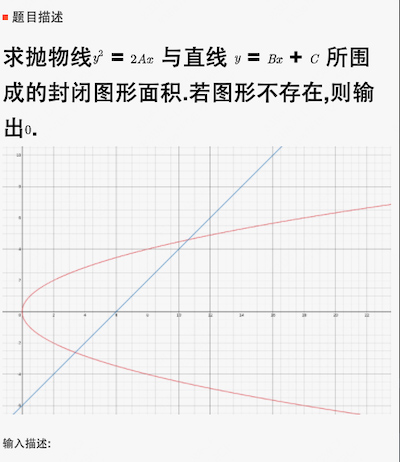
这个题目本来是跟积分相关的,代入化简得到其一元二次的形式 $B^2x^2+(2BC-2A)x+C^2=0$,用求根公式得俩解x1,x2:
思路是可以从求梯形面积 - 曲线与y轴的积分面积 $\int_{y_1}^{y_2} y^2/2A \mathrm{dy}$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| int main() {
float A,B,C;
cin>>A>>B>>C;
if( (4 * pow(A, 2) - 8 * A * B * C) < 0){
cout<<"0"<<endl;
return 0;
};
float x1=0.0, x2=0.0, area=0.0;
if(C == 0){
if(A<0) A = -A;
if(B<0) B = -B;
x1 = 0;
x2 = 2*A/pow(B, 2);
area = 0.5 * abs(x2) * sqrt(abs(2*A*x2)) - pow((sqrt(abs(2*A*x2))),3)/6/A;
cout<<x1<<" "<<x2<<" "<<area<<endl;
}
else{
x1 = ((2*A-2*B*C) + sqrt(4*pow(A, 2) - 8*A*B*C))/2*pow(B, 2);
x2 = ((2*A-2*B*C) - sqrt(4*pow(A, 2) - 8*A*B*C))/2*pow(B, 2);
float y1,y2;
y1 = B*x1+C;
y2 = B*x2+C;
area = y1>y2? (abs(x1) + abs(x2)) * (y1-y2) * 0.5 - (pow(y1, 3) - pow(y2, 3))/6/A : (abs(x1) + abs(x2)) * (y2-y1) * 0.5 - (pow(y2, 3) - pow(y1, 3))/6/A;
cout<<x1<<" "<<x2<<" "<<area<<endl;
}
return 0;
}
|
Reference
1,华为8.26笔试题
2,腾讯笔试题


